
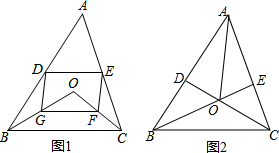
 点D,E分别是△ABC的边AB,AC的中点.
点D,E分别是△ABC的边AB,AC的中点.分析 (1)由三角形中位线定理得出DE∥GF,DE=GF,即可得出结论;
(2)由三角形的重心定理即可得出结论.
解答 (1)证明:∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
同理:GF∥BC,BC=2GF,
∴DE∥GF,DE=GF,
∴四边形DEFG是平行四边形;
(2)解:AO的延长线经过BC的中点;理由如下:
∵BE、CD是△ABC的中线,BE交DC于点O,三角形的三条中线相交于一点,
∴AO的延长线经过BC的中点.
点评 本题考查了三角形的中位线定理、平行四边形的判定、三角形的重心定理;熟记三角形的中位线平行于第三边并且等于第三边的一半是解决问题(1)的关键.


科目:初中数学 来源: 题型:选择题
| A. | 中位数是27 | B. | 众数是23和26 | C. | 极差是6 | D. | 平均数是24.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
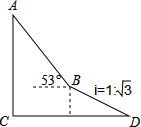 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
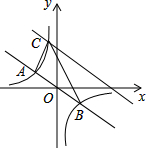 如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
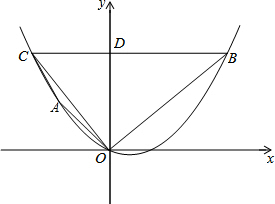 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(-1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(-1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com