
【题目】定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于135°.下面,我们来研究它的一些性质与判定:
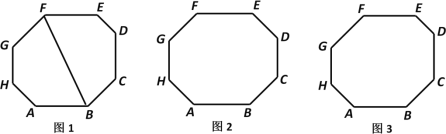
(1)如图1,等角八边形ABCDEFGH中,连结BF.
①请直接写出∠ABF+∠GFB的度数.
②求证:AB∥EF.
③我们把AB与EF称为八边形的一组正对边.由②同理可得:BC与FG,CD与GH,DE与HA这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
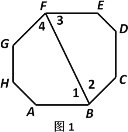
(2)如图2,等角八边形ABCDEFGH中,如果有AB=EF,BC=FG,则其余两组正对边CD与GH,DE与HA分别相等吗?证明你的结论.
(3)如图3,八边形ABCDEFGH中,若四组正对边分别平行,则显然有∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.请探究:该八边形至少需要已知几个内角为135°,才能保证它一定是等角八边形?
【答案】(1)①∠ABF+∠GFB=135°;②详见解析;③等角八边形的每一组正对边平行;(2)CD=GH,DE=HA,详见解析;(3)结论:至少需要已知5个内角为135°
【解析】
(1)①由等角八边形的概念可得它的每个内角均为135°,五边形BAHGF的内角和为540°,减去(∠A+∠H+∠G),即可求得结论;
②根据“内错角相等,两直线平行”即可证明;
③根据题目提供的信息,总结出结论即可;
(2)分别证明四边形ABEF是平行四边形,△AFG≌△EBC,△AGH≌△ECD即可得到结论;
(3)若4个内角等于135°,则每个内角不一定都为135°,若5个内角等于135°,其余各角的度数也是135°.
(1)①五边形BAHGF的内角和为(5-2)×180°=540°
∵∠A=∠H=∠G=![]()
∴∠ABF+∠GFB=540°-(∠A+∠H+∠G)=135°
即∠ABF+∠GFB=135°.
②∵∠1+∠4=135°,∠GFE=∠3+∠4=135°,
∴∠1=∠3,
∴AB∥EF.
③等角八边形的每一组正对边平行.
(2)如图2,连结AF,BE,AG,CE,由①得:AB∥EF,
∵AB=EF,
∴四边形ABEF是平行四边形,
∴AF=BE,AF∥BE,
又∵BC∥FG,
∴∠AFG=∠EBC,
又∵BC=FG,
∴△AFG≌△EBC,
∴AG=EC,∠AGF=∠ECB,
∵∠HGF=∠BCD=135°,
∴∠AGH=∠ECD,
又∵∠H=∠D=135°,
∴△AGH≌△ECD,
∴CD=GH,DE=HA.
(3)结论:至少需要已知5个内角为135°.
①若4个内角等于135°,则每个内角不一定都为135°,
如图4,八边形ABCMNFPH不是等角八边形;
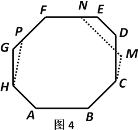
②若5个内角等于135°:
∵∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.
∴这八个角中,不论已知哪5个角是135°,都可以推导出其余的内角也是135°.


科目:初中数学 来源: 题型:
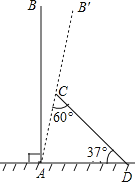
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
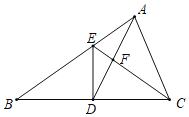
【题目】如图,在△ABC中,AD是BC边上的中线,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)过点A作AM⊥BC于点M,求DE:AM的值;
(3)若S△FCD=5,BC=10,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)交x轴于A,B两点(A在B的左侧),交y轴于点C,抛物线的顶点为P,过点B作BC的垂线交抛物线于点D.
(1)若点P的坐标为(-4,-1),点C的坐标为(0,3),求抛物线的表达式;
(2)在(1)的条件下,求点A到直线BD的距离;
(3)连接DC,若点P的坐标为(-![]() ,-
,-![]() ),DC∥x轴,则在x轴上方的抛物线上是否存在点M,使∠AMB=∠BDC?若存在,求出点M的坐标;若不存在,请说明理由.
),DC∥x轴,则在x轴上方的抛物线上是否存在点M,使∠AMB=∠BDC?若存在,求出点M的坐标;若不存在,请说明理由.
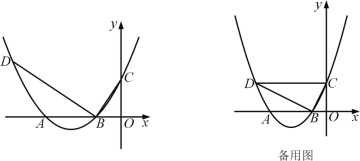
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
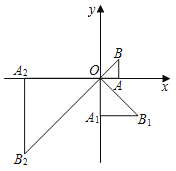
【题目】如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋90°转得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O,…,依此规律,得到等腰直角三角形A2020OB2020,则点B2020的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点A在抛物线y=-x2+2x+3(0≤x≤3)上运动,直线l经过点(0,6),且与y轴垂直,过点A作AC⊥l于点C,以AC为对角线作矩形ABCD,则另一对角线BD的取值范围正确的是( )

A.2≤BD≤3B.3≤BD≤6C.1≤BD≤6D.2≤BD≤6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F两点分别在平行四边形ABCD的边CD、AD上,AE=CF,AE、CF相交于点O.
(1)用尺规作出∠AOC的角平分线OM(保留作图痕迹,不写作法);
(2)求证:OM一定经过B点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
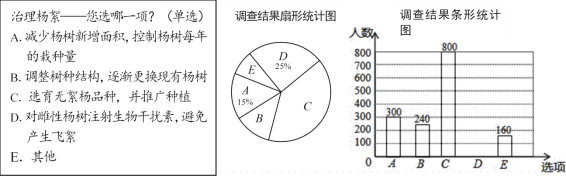
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 °;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com