
 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
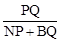 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.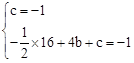 ,解得
,解得 。
。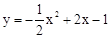 。
。 。
。 ,解得
,解得 ,
,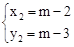 。
。 =AP0。
=AP0。 (即为PQ的长),
(即为PQ的长), 。
。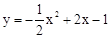 于点M,则M为符合条件的点。
于点M,则M为符合条件的点。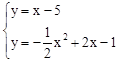 ,得:
,得: ,
,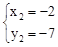 。
。
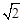 .
.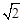 。
。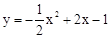 于点M,则M为符合条件的点。
于点M,则M为符合条件的点。 ,得:
,得: ,
, 。
。 ,
,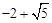 ),M4(
),M4( ,
,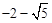 )。
)。 ,
,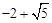 ),M4(
),M4( ,
,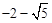 )。
)。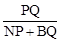 存在最大值。理由如下:
存在最大值。理由如下: 为定值,则当NP+BQ取最小值时,
为定值,则当NP+BQ取最小值时,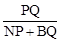 有最大值。
有最大值。
 。
。 。
。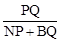 的最大值为
的最大值为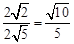 。
。 .此时,将直线AC向右平移4个单位后所得直线(y=x﹣5)与抛物线的交点,即为所求之M点。
.此时,将直线AC向右平移4个单位后所得直线(y=x﹣5)与抛物线的交点,即为所求之M点。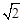 .此时,将直线AC向右平移2个单位后所得直线(y=x﹣3)与抛物线的交点,即为所求之M点.
.此时,将直线AC向右平移2个单位后所得直线(y=x﹣3)与抛物线的交点,即为所求之M点. 为定值,因此当NP+BQ取最小值时,
为定值,因此当NP+BQ取最小值时,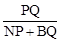 有最大值。如答图2所示,作点B关于直线AC的对称点B′,由解析可知,当B′、Q、F(AB中点)三点共线时,NP+BQ最小,最小值为线段B′F的长度。
有最大值。如答图2所示,作点B关于直线AC的对称点B′,由解析可知,当B′、Q、F(AB中点)三点共线时,NP+BQ最小,最小值为线段B′F的长度。

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
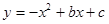 的顶点为Q,与
的顶点为Q,与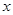 轴交于A(-1,0)、B(5, 0)两点,与
轴交于A(-1,0)、B(5, 0)两点,与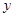 轴交于C点.
轴交于C点.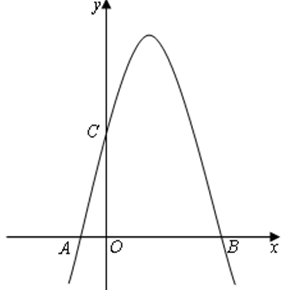
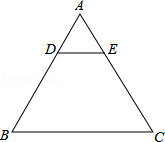
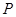 ,使得△
,使得△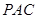 的周长最小.请在图中画出点
的周长最小.请在图中画出点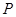 的位置,并求点
的位置,并求点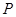 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.(0,0) | B.(1,﹣1) | C.(0,﹣1) | D.(﹣1,﹣1) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:| x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;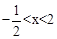 时,y<0;
时,y<0; 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.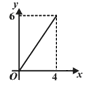 | B.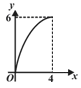 | C.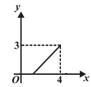 | D.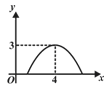 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com