
【题目】如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 ![]() .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′. 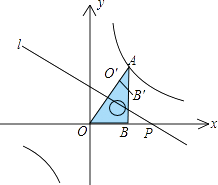
(1)当点O′与点A重合时,点P的坐标是;
(2)设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
【答案】
(1)(4,0)
(2)4≤t≤2 ![]() 或﹣2
或﹣2 ![]() ≤t≤﹣4
≤t≤﹣4
【解析】解:(1.)当点O′与点A重合时 
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O′B′.
AP=OP,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
故答案为:(4,0).
(2.)由(1)知,当P的坐标是(4,0)时,直线OB与双曲线有交点O′,
当B′在双曲线上时,作B′C⊥OP于C,
∵BP=B′P,∠B′BP=60°,
∴△BB′P是等边三角形,
∴BP=B′P=t﹣2,
∴CP= ![]() (t﹣2),B′C=
(t﹣2),B′C= ![]() (t﹣2),
(t﹣2),
∴OC=OP﹣CP= ![]() t+1,
t+1,
∴B′的坐标是( ![]() t+1,
t+1, ![]() (t﹣2)),
(t﹣2)),
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2 ![]() ,
,
∴A(2,2 ![]() ),
),
∵A和B′都在双曲线上,
∴( ![]() t+1)
t+1) ![]() (t﹣2))=2×2
(t﹣2))=2×2 ![]() ,
,
解得:t=±2 ![]() ,
,
∴t的取值范围是4≤t≤2 ![]() 或﹣2
或﹣2 ![]() ≤t≤﹣4.
≤t≤﹣4.
故答案为:4≤t≤2 ![]() 或﹣2
或﹣2 ![]() ≤t≤﹣4.
≤t≤﹣4.
(1)当点O′与点A重合时,即点O与点A重合,进一步解直角三角形AOB,利用轴对称的现在解答即可;(2)分别求出O′和B′在双曲线上时,P的坐标即可.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
-4,![]() ,0,
,0,![]() ,-3.14,717,-(+5),+1.88,
,-3.14,717,-(+5),+1.88,![]()
(1)正数集合:{ … };
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)分数集合:{ … }.
查看答案和解析>>
科目:初中数学 来源: 题型:
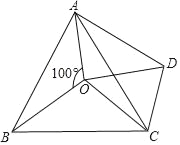
【题目】如图,O在等边△ABC内,∠AOB=100°,∠BOC=x,将△BOC绕点C顺时针旋转60°,得△ADC,连接OD.
(1)△COD的形状是 ;
(2)当x=150°时,△AOD的形状是 ;此时若OB=3,OC=5,求OA的长;
(3)当x为多少度时,△AOD为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:(1)13=![]() ×12×22;(2)13+23=
×12×22;(2)13+23=![]() ×22×32;(3)13+23+33=
×22×32;(3)13+23+33=![]() ×32×42;(4)13+23+33+43=
×32×42;(4)13+23+33+43=![]() ×42×52;
×42×52;![]()
根据上述等式的规律,解答下列问题:
(1)写出第5个等式:_____;
(2)写出第n个等式(用含有n的代数式表示);
(3)设s是正整数且s≥2,应用你发现的规律,化简:![]() ×s2×(s+1)2﹣
×s2×(s+1)2﹣![]() ×(s﹣1)2×s2.
×(s﹣1)2×s2.
查看答案和解析>>
科目:初中数学 来源: 题型:
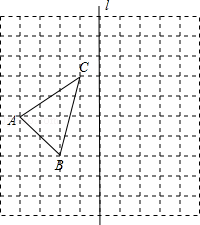
【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线.若∠A1=α,则∠A2019=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图1.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图2,当∠COD在∠AOB的外部时,(1)中∠AOC与∠DOE的数量关系还成立吗?若成立,请推导出∠AOC与∠DOE的度数之间的关系;若不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com