
【题目】已知x2﹣8x+16﹣m2=0(m≠0)是关于x的一元二次方程
(1)证明:此方程总有两个不相等的实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c是该方程的两个实数根,求△ABC的面积.
【答案】(1)证明见解析;(2)△ABC的面积为![]() .
.
【解析】
(1)计算判别式的值得到△=4m2,从而得到△>0,然后根据判别式的意义得到结论;
(2)利用求根公式解方程得到x=4±m,即b=4+m,c=4﹣m,讨论:当b=a=6时,即4+m=6,解得m=2,利用勾股定理计算出底边上的高,然后计算△ABC的面积;当c=a时,即4﹣m=6,解得m=﹣2,即a=c=6,b=2,利用同样方法计算△ABC的面积.
(1)证明:△=(﹣8)2﹣4×(16﹣m2)
=4m2,
∵m≠0,
∴m2>0,
∴△>0,
∴此方程总有两个不相等的实数根;
(2)解:∵![]()
∴![]() ,
,
即b=4+m,c=4﹣m,
∵m≠0
∴b≠c
当b=a时,4+m=6,解得m=2,即a=b=6,c=2,
如图,AB=AC=6,BC=2,AD为高,
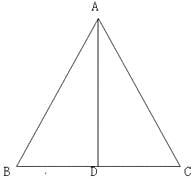
则BD=CD=1,
∴![]()
∴△ABC的面积为:![]() ×2×
×2×![]() =
=![]() ;
;
当c=a时,4﹣m=6,解得m=﹣2,即a=c=6,b=2,
如图,AB=AC=6,BC=2,AD为高,

则BD=CD=1,
∴![]()
∴△ABC的面积为:![]() ×2×
×2×![]() =
=![]() ,
,
即△ABC的面积为![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
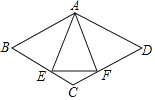
【题目】如图,在菱形ABCD中,点E,F分别在BC,CD上,且CE=CF,
(1)求证△ABE≌△ADF.
(2)若∠B=50°,AE⊥BC,求∠AEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P为AB延长线上一点,PC切⊙O于点C,过点B作BE∥PC交⊙O于点E,连接CE,CB.
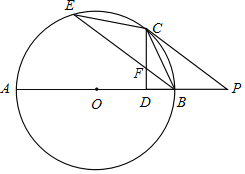
(1)试判断△BCE的形状,并说明理由;
(2)过点C作CD⊥AB于点D交BE于点F,若cosP=![]() ,CF=5,求AB的长.
,CF=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】样本一:92,94,96;样本二:m,94,96.嘉淇通过相关计算并比较,发现:样本二的平均数较大,方差较小.则m的值可能是( )
A.91B.92C.95D.98
查看答案和解析>>
科目:初中数学 来源: 题型:
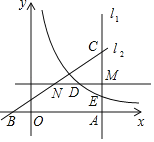
【题目】如图,直线l1经过点A(6,0),且垂直于x轴,直线l2:y=kx+b(b>0)经过点B(﹣2,0),与l1交于点C,S△ABC=16.点M是线段AC上一点,直线MN∥x轴,交l2于点N,D是MN的中点.双曲线y=![]() (x>0)经过点D,与l1交于点E.
(x>0)经过点D,与l1交于点E.
(1)求l2的解析式;
(2)当点M是AC中点时,求点E的坐标;
(3)当MD=1时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的门框上装有一把防盗门锁(如图1).其平面结构图如图2所示,锁身可以看成由两条等弧AD,弧BC和矩形ABCD组成,弧BC的圆心是倒锁按钮点M.已知弧AD的弓形高GH=2cm,AD=8cm,EP=11cm.当锁柄PN绕着点N旋转至NQ位置时,门锁打开,此时直线PQ与弧BC所在的圆相切,且PQ∥DN,tan∠NQP=2.
(1)弧BC所在圆的半径为_____cm.
(2)线段AB的长度约为_____cm.(![]() ≈2.236,结果精确到0.1cm)
≈2.236,结果精确到0.1cm)
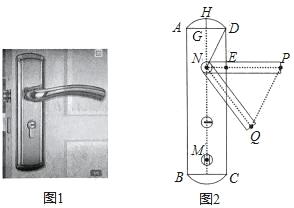
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为定值,E是边CD上的动点(不与点C,D重合),AE交对角线BD于点F,FG⊥AE交BC于点G,GH⊥BD于点H.现给出下列命题:①AF=FG;②FH的长度为定值.则( )
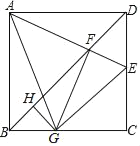
A.①是真命题,②是真命题B.①是真命题,②是假命题
C.①是假命题,②是真命题D.①是假命题,②是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.CP=![]() ,PD=6.如果点M是OP的中点,则DM的长是_____.
,PD=6.如果点M是OP的中点,则DM的长是_____.
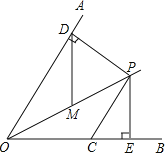
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线;以BC为直径的⊙O交BD于点E,连接CE并延长交AB于点F,连接DF,
(1)补全图中图形;(要求:清晰、准确,标出相应字母,不写作法,不必保留作图痕迹)
(2)DC=DF;
(3)若AC=8,BC=6,求CF的长.
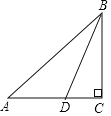
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com