
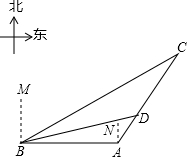
 ���꣬�ҹ��������������������������Υ���ж�������ѡ������������ڹ���֮�⣮��ͼ��ij���ҹ�һ�Һ��ബѲ����A�ۿ���������B��ʱ��������B�ı�ƫ��60�㷽�����150���ﴦ��C����һ���ɴ�ֻ����CA������ʻ��C����A�ۿڵı�ƫ��30�㷽���ϣ����ബ��A�ۿڷ���ָ�ִ����������A�ۿ���AC����ʻ������D���ɹ����ؿ��ɴ�ֻ����ʱD����B��ľ���Ϊ75$\sqrt{2}$���
���꣬�ҹ��������������������������Υ���ж�������ѡ������������ڹ���֮�⣮��ͼ��ij���ҹ�һ�Һ��ബѲ����A�ۿ���������B��ʱ��������B�ı�ƫ��60�㷽�����150���ﴦ��C����һ���ɴ�ֻ����CA������ʻ��C����A�ۿڵı�ƫ��30�㷽���ϣ����ബ��A�ۿڷ���ָ�ִ����������A�ۿ���AC����ʻ������D���ɹ����ؿ��ɴ�ֻ����ʱD����B��ľ���Ϊ75$\sqrt{2}$������� ��1������B��BH��CA��CA���ӳ����ڵ�H���������Ǻ�������BH�ij���Ϊ����
��2�����ݹ��ɶ�������DH����Rt��ABH�У��������Ǻ�������AH����һ���õ�AD�ij���
��� 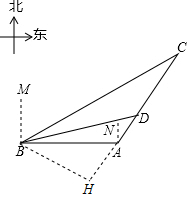 �⣺��1������B��BH��CA��CA���ӳ����ڵ�H��
�⣺��1������B��BH��CA��CA���ӳ����ڵ�H��
�ߡ�MBC=60�㣬
���CBA=30�㣬
�ߡ�NAD=30�㣬
���BAC=120�㣬
���BCA=180��-��BAC-��CBA=30�㣬
��BH=BC��sin��BCA=150��$\frac{1}{2}$=75�������
��B�㵽ֱ��CA�ľ�����75���
��2����BD=75$\sqrt{2}$���BH=75���
��DH=$\sqrt{B{D}^{2}-B{H}^{2}}$=75���
�ߡ�BAH=180��-��BAC=60�㣬
��Rt��ABH��tan��BAH=$\frac{BH}{AH}$=$\sqrt{3}$��
��AH=25$\sqrt{3}$���
��AD=DH-AH=��75-25$\sqrt{3}$���������
��ִ������A��D�����ˣ�75-25$\sqrt{3}$�����
���� ������Ҫ�����˹��ɶ�����Ӧ�ã���ֱ�������ε�Ӧ��-��������⣬����Ӧ��������Ǻ�����ϵ�ǽ���ؼ���


 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У�����A��AE��BC�ڵ�E��AF��DC�ڵ�F��AE=AF��
��ͼ����?ABCD�У�����A��AE��BC�ڵ�E��AF��DC�ڵ�F��AE=AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | �� | �� | �� | |
| ƽ���ɼ������� | 8.6 | 8.4 | 8.6 | 7.6 |
| ���� | 0.94 | 0.74 | 0.56 | 1.92 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com