
【题目】(本小题满分8分)如图,点E、F为线段BD的两个三等分点,四边形AECF是菱形.
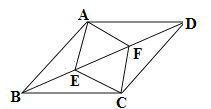
(1)试判断四边形ABCD的形状,并加以证明;
(2)若菱形AECF的周长为20,BD为24,试求四边形ABCD的面积.
【答案】(1)四边形ABCD为菱形,证明过程见解析;(2)S四边形ABCD=72.
【解析】
试题分析:(1)连接AC,根据菱形的对角线互相垂直平分可得AC⊥BD,AO=OC,EO=OF,再求出BO=OD,然后根据对角线互相垂直平分的四边形是菱形证明;
(2)根据菱形的四条边都相等求出边长AE,根据菱形的对角线互相平分求出OE,然后利用勾股定理列式求出AO,再求出AC,最后根据菱形的面积等于对角线乘积的一半列式计算即可得解.
试题解析:
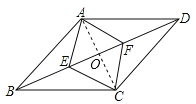
解:(1)四边形ABCD为菱形.
理由如下:如图,连接AC交BD于点O,
∵四边形AECF是菱形,
∴AC⊥BD,AO=OC,EO=OF .
又∵点E、F为线段BD的两个三等分点,
∴BE=FD,
∴BO=OD .
∵AO=OC,
∴四边形ABCD为平行四边形 .
∵AC⊥BD,
∴四边形ABCD为菱形;
(2)∵四边形AECF为菱形,且周长为20,∴AE=5 .
∵BD=24,∴EF=8,OE=![]() EF=
EF=![]() ×8=4.
×8=4.
由勾股定理得,AO=![]() =
=![]() =3,
=3,
∴AC=2AO=2×3=6 .
∴S四边形ABCD=![]() BDAC=
BDAC=![]() ×24×6=72.
×24×6=72.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中O是原点,平行四边形ABCO的顶点A、C的坐标分别(8,0)、(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是![]() ;④
;④![]() .正确的个数是( )
.正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
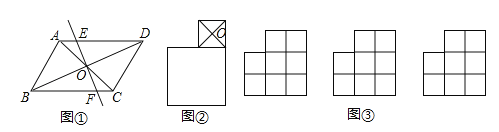
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.
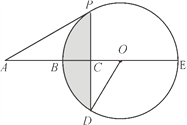
(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生对待学习的态度一直是教育工作者关注的问题之一.为此市教育局对部分学校的九年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1) 此次抽样调查中,共调查了 名学生;并将图①补充完整;
(2) 求出图中②C级所占的圆心角的度数;
(3) 根据抽样调查结果,请你估计我市近50000名九年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
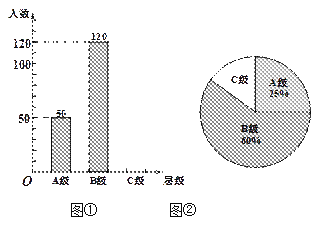
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若|a|=﹣a,则a<0
B. 式子3xy2﹣43x3y+12是七次三项式
C. 若a=b,m是有理数,则![]()
D. 若abcd<0,a+b=0,cd>0,那么这四个数中负因数的个数至少有1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com