
【题目】在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画等腰三角形,要求三个顶点都在格点上(小正方形的顶点称为格点),用实线画四种图形,且分别符合下列各条件:
(1)面积为2(画在图1中);
(2)面积为4,且三边与AB或AD都不平行(画在图2中);
(3)面积为5,且三边与AB或AD都不平行(画在图3中);
(4)面积为![]() ,且三边与AB或AD都不平行(画在图4中).
,且三边与AB或AD都不平行(画在图4中).
【答案】(1)见解析;(2)见解析;(3)见解析;(4)见解析
【解析】
(1)利用等腰三角形的对称性,计算等腰三角形的面积可求图形;
(2)利用等腰三角形的对称性,计算等腰三角形的面积可求图形;
(3)利用等腰三角形的对称性,计算等腰三角形的面积可求图形;
(4)利用等腰三角形的对称性,计算等腰三角形的面积可求图形.
解:(1)如图1
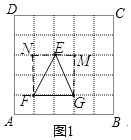
∵ME=EN,MG=FN,∠EMG=∠FNE=90°
∴△EMG≌△EFN
∴EG=EF
∴△EFG是等腰三角形
∵S△EFG=![]() ×2×2=2
×2×2=2
∴△EFG为所求等腰三角形.
(2)如图2
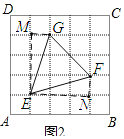
∵ME=EN,MG=FN,∠EMG=∠FNE=90°
∴△EMG≌△EFN
∴EG=EF
∴△EFG是等腰三角形
∵S△EFG=3×3﹣2×![]() =4
=4
∴△EFG为所求等腰三角形.
(3)如图3
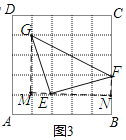
∵ME=EN,MG=FN,∠EMG=∠FNE=90°
∴△EMG≌△EFN
∴EG=EF
∴△EFG是等腰三角形
∵S△EFG=3×4﹣2×![]() =5
=5
∴△EFG为所求三角形.
(4)如图4
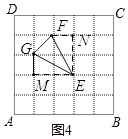
∵ME=EN,MG=FN,∠EMG=∠FNE=90°
∴△EMG≌△EFN
∴EG=EF
∴△EFG是等腰三角形
∵S△EFG=2×2﹣2×![]() ×2×1﹣
×2×1﹣![]() ×1×1=
×1×1=![]()
∴△EFG为所求等腰三角形


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】在一个口袋里装着白、红、黑三种颜色的小球(除颜色外形状大小完全相同),其中白球3个、红球2个、黑球1个.
(1)随机从袋中取出一个球,求取出的球是黑球的概率;
(2)若取出的第一只球是红球,不将它放回袋里,从袋中余下的球中再随机地取出1个,这时取出的球是黑球的概率是多少?
(3)若取出一个球,将它放回袋中,从袋中再随机地取出一个球,两次取出的球都是白球的概率是多少?(用列表法或树状图计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
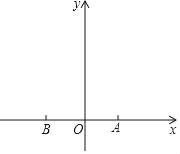
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),点A关于原点的对称点为点B.
(1)求点B的坐标;
(2)若以AB为一边向上作有一个角为30°的直角三角形ABC,在给出的直角坐标系中作出所有的符合条件的六个三角形;
(3)将所作三角形中你认为好计算的两个C点的坐标求出来或直接写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,能用AAS来判定△ACD≌△ABE需要添加的条件是( )
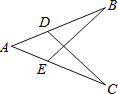
A.∠AEB=∠ADC,BE=CDB.AC=AB,∠B=∠C
C.AC=AB,AD=AED.∠AEB=∠ADC,∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+4的图象分别与x轴、y轴交于点A,B.
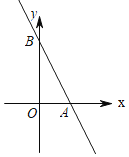
(1)求△AOB的面积;
(2)在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
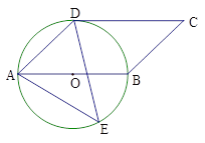
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点,且CD切⊙O于点D.
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求△ADE面积的最大值.
cm,试求△ADE面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一书架上的方格中放置四本厚度和长度相同的书,其中书架方格长BF=40cm,书的长度AB=20cm,设一本书的厚度为xcm.
(1)如图1左边三本书紧贴书架方格内侧竖放,右边一本书自然向左斜放,支撑点为C,E,最右侧书一个角正好靠在方格内侧上,若CG=4cm,求EF的长度;
(2)如图2左边两本书紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,最右侧书的下面两个角正好靠在方格内上,若∠DCE=30°,求x的值(保留一位小数).(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定了每月用水量不超过18立方米和超过18立方米两种不同的收费标准,该市的用户每月应交水费![]() (元)是用水量
(元)是用水量![]() (立方米)的一次函数,其图象如图所示:
(立方米)的一次函数,其图象如图所示:
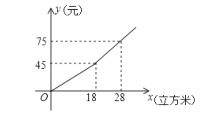
(1)若某月用水量超过18立方米,则每立方米的水费为__________元;
(2)当![]() 时,
时,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若小敏家三月份交水费81元,求这个月小敏家的用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com