
【题目】已知![]() ,
,![]() 关于
关于![]() 的方程
的方程![]() 的两个实数根.
的两个实数根.
(1)若![]() 时,求
时,求![]() 的值;
的值;
(2)若等腰![]() 的一边长
的一边长![]() ,另两边长为
,另两边长为![]() 、
、![]() ,求
,求![]() 的周长.
的周长.
【答案】(1)30;(2)5
【解析】
(1)若k=3时,方程为x2-5x+6=0,方法一:先求出一元二次方程的两根a,b,再将a,b代入因式分解后的式子计算即可;方法二:利用根与系数的关系得到a+b=5,ab=6,再将![]() 因式分解,然后利用整体代入的方法计算;
因式分解,然后利用整体代入的方法计算;
(2)分1为底边和1为腰两种情况讨论即可确定等腰三角形的周长.
解:(1)将![]() 代入原方程,
代入原方程,
得:![]() .
.
方法一:
解上述方程得:![]()
因式分解,得:![]() .
.
代入方程的解,
得:![]() .
.
方法二:应用一元二次方程根与系数的关系
因式分解,
得:![]() ,
,
由根与系数的关系,得![]() ,
,
则有:![]() .
.
(2)①当![]() 与
与![]() 其中一个相等时,不妨设
其中一个相等时,不妨设![]() ,
,
将![]() 代回原方程,得
代回原方程,得![]() .
.
解得:![]() ,
,
此时![]() ,不满足三角形三边关系,不成立;
,不满足三角形三边关系,不成立;
②当![]() 时,
时,![]() ,
,
解得:![]() ,
,
解得:![]() ,
,
![]() .
.
综上所述:△ABC的周长为5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为减少环境污染,提高生产效率,公司计划对A、B两类生产线全部进行改造.改造一条A类生产线和两条B类生产线共需资金200万元;改造两条A类生产线和一条B类生产线共需资金175万元.
(1)改造一条A类生产线和一条B类生产线所需的资金分别是多少万元?
(2)公司计划今年对A,B两类生产线共6条进行改造,改造资金由公司自筹和国家财政补贴共同承担.若今年公司自筹的改造资金不超过320万元;国家财政补贴投入的改造资金不少于70万元,其中国家财政补贴投入到A、B两类生产线的改造资金分别为每条10万元和15万元.请你通过计算求出有几种改造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标为
图象的一部分,抛物线的顶点坐标为![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,点
,点![]() 和点
和点![]() 均在直线
均在直线![]() 上.①
上.①![]() ;②
;②![]() ;③抛物线与
;③抛物线与![]() 轴的另一个交点时
轴的另一个交点时![]() ;④方程
;④方程![]() 有两个不相等的实数根;⑤
有两个不相等的实数根;⑤![]() ;⑥不等式
;⑥不等式![]() 的解集为
的解集为![]() .
.
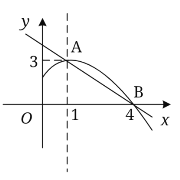
上述六个结论中,其中正确的结论是_____________.(填写序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.
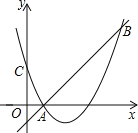
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则![]() 的最小值是( )
的最小值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有( )
A.0种B.1种C.2种D.3种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以1.5m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图(2)所示.
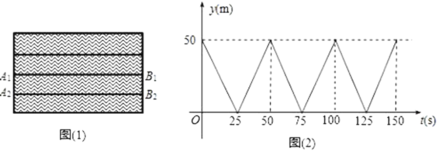
(1)赛道的长度是 m,甲的速度是 m/s;当t= s时,甲、乙两人第一次相遇,当t= s时,甲、乙两人第二次相遇?
(2)第三次相遇时,两人距池边B1B2多少米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com