练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知∠PAB＝，在∠PAB的角平分线AC上取一点O，使OA＝3cm，分别以下列条件作⊙O，试判断PA与⊙O的位置关系．

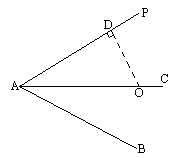
    (1)以O为圆心，1cm为半径作圆；

    (2)以O为圆心，1.5cm为半径作圆；

    (3)以O为圆心，2cm为半径作圆．

    答案：
    解析：

    　　解　　作OD⊥PA于D．

    　　因为∠PAB＝，AC为∠PAB的角平分线，所以

    　　∠PAC＝∠PAB＝，

    　　OD＝AO＝×3＝1.5(cm)．

    　　(1)因为OD＞1cm，所以PA与⊙O相离．

    　　(2)因为OD＝1.5cm，所以PA与⊙O相切．

    　　(3)因为OD＜2cm，所以PA与⊙O相交．

    　　分析　　要判断直线与圆的位置关系，只需判断圆心到直线的距离与半径的大小关系．本题中可根据含角的直角三角形的特殊性质，计算出点O到PA的距离．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：中考备考专家数学(第二版) 题型：044

    如图，已知矩形ABCB中，CH⊥BD于点H，P为AD上的一个动点(点P与点A、D不重合)，CP与BD交于点E，若CH＝，DH∶CD＝5∶13，设AP＝x，四边形ABEP的面积为y．

    (1)求BD的长；

    (2)求y与x的函数关系式，并写出自变量x的取值范围；

    (3)当四边形ABEP的面积是△PED面积的5倍时，连结BP，判断△PAB与△PDC是否相似，如果相似，求出相似比；如果不相似，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书　九年级数学　上　（江苏版课标本） 江苏版课标本 题型：044

    如图，已知PAB是⊙O的割线，AB为⊙O的直径，PC为⊙O的切线，C为切点，BD⊥PC于点D，交⊙O于点E，PA＝AO＝OB＝1．

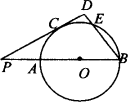
    (1)求∠P的度数；

    (2)求DE的长．

    查看答案和解析>>

    科目：初中数学 来源：初中数学解题思路与方法 题型：044

    如图，已知PAB、PCD是⊙O的两条割线，∠P＝40°，且，连结AD，求∠ADP度数．

    查看答案和解析>>

    科目：初中数学 来源：2006年浙江省湖州市初中毕业生学业考试数学试卷(华师大实验区) 题型：059

    如图，已知平面直角坐标系，A、B两点的坐标分别为A(2，－3)，B(4，－1)．

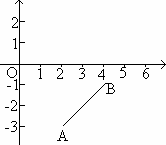
    (1)若P(p，0)是x轴上的一个动点，则当p＝________时，△PAB的周长最短；

    (2)若C(a，0)，D(a＋3，0)是x轴上的两个动点，则当a＝________时，四边形ABDC的周长最短；

    (3)设M，N分别为x轴和y轴上的动点，请问：是否存在这样的点M(m，0)、N(0，n)，使四边形ABMN的周长最短？若存在，请求出m＝________，n＝________(不必写解答过程)；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案