
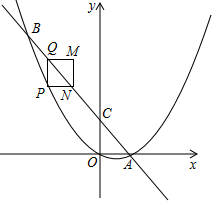
 抛物线y=ax2+bx与直线y=mx+n交于点A(1,0),B(-2,6),点P是直线AB下方抛物线上的一个动点.
抛物线y=ax2+bx与直线y=mx+n交于点A(1,0),B(-2,6),点P是直线AB下方抛物线上的一个动点.分析 (1)将点A、B坐标代入y=ax2+bx求出a、b即可得;
(2)根据A、B坐标求得直线解析式,令Q(x,y1)、P(x,y2),得出QP=y1-y2=(-2x+2)-(x2-x)=-x2-x+2,由△QPN∽△COA且OA=$\frac{1}{2}$OC知PN=$\frac{1}{2}$PQ=$\frac{1}{2}$(-x2-x+2),根据矩形的周长=2(PQ+PN)列出解析式,并配方即可得最大值;
(3)如图,设P(x,y),知BD=|6-y|、PD=|x+2|、PE=|y|、AE=|1-x|,由PA=PB即BD2+PD2=PE2+AE2得4y-2x-13=0,将y=x2-x代入求得x即可.
解答 解:(1)∵抛物线y=ax2+bx过点A(1,0),B(-2,6),
∴$\left\{\begin{array}{l}{a+b=0}\\{4a-2b=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,
∴抛物线解析式为y=x2-x;
(2)∵直线y=mx+n过点A(1,0),B(-2,6),
∴$\left\{\begin{array}{l}{m+n=0}\\{-2m+n=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-2}\\{n=2}\end{array}\right.$,
∴直线解析式为y=-2x+2,
令Q(x,y1)、P(x,y2),
则QP=y1-y2=(-2x+2)-(x2-x)=-x2-x+2,
∵直线y=-2x+2与x轴的交点A(1,0)、与y轴的交点(0,2),
∴OA=$\frac{1}{2}$OC,
∵PQ∥y轴,PN∥x轴,
∴△QPN∽△COA,
∴PN=$\frac{1}{2}$PQ=$\frac{1}{2}$(-x2-x+2),
则矩形的周长=2(PQ+PN)=2[-x2-x+2+$\frac{1}{2}$(-x2-x+2)]=-3x2-3x+6=-3(x+$\frac{1}{2}$)2+$\frac{27}{4}$,
∴矩形周长的最大值为$\frac{27}{4}$;
(3)如图,过点P作PE⊥x轴于点E,过点B作BF⊥x轴于点F,作PD⊥BF于点D,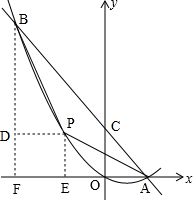
设P(x,y),
则BD=|6-y|、PD=|x+2|、PE=|y|、AE=|1-x|,
∵PA=PB,
∴BD2+PD2=PE2+AE2,
即(6-y)2+(2+x)2=y2+(1-x)2,
整理,得:4y-2x-13=0,
又y=x2-x,
∴4(x2-x)-2x-13=0,
解得:x1=$\frac{3-\sqrt{61}}{4}$,x2=$\frac{3+\sqrt{61}}{4}$>1(舍去),
∴y=$\frac{29-\sqrt{61}}{8}$,
∴点P($\frac{3-\sqrt{61}}{4}$,$\frac{29-\sqrt{61}}{8}$).
点评 本题主要考查二次函数的综合问题,熟练掌握待定系数法求函数解析式、相似三角形的判定与性质、勾股定理等知识点是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
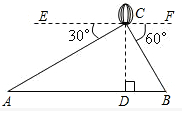 如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
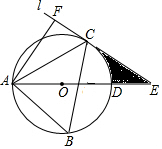 如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.
如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com