
【题目】大石桥市政府为了落实“暖冬惠民工程”,计划对城区内某小区的部分老旧房屋及供暖管道和部分路段的人行地砖、绿化带等公共设施进行全面更新改造。该工程乙队单独完成所需天数是甲队单独完成所需天数的1.5倍 , 若甲队先做10天,剩下两队合作30天完成。
(1)甲乙两个队单独完成此项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙对每天的施工费用为5.6万元,工程施工的预算费用为500万元,为了缩短工期并高效完成工程,拟预算的费用是否够用?若不够用,需追加预算多少万元?请说明理由。
【答案】(1)甲队单独完成此项工程需要60天,乙队单独完成此项工程需要90天;(2)工程预算的施工费用不够用,需追加预算4万元.
【解析】
(1)设甲单独完成这项工程所需天数,表示出乙单独完成这项工程所需天数及各自的工作效率.根据工作量=工作效率×工作时间列方程求解;
(2)根据题意,甲乙合作工期最短,所以须求合作的时间,然后计算费用,作出判断.
(1)设此工程甲队单独完成需x天,则乙队单独完成这项工程需1.5x天.由题意:
![]()
解得:x=60.
经检验,x=60是原方程的解,且适合题意.
1.5x=1.5×60=90.
答:甲队单独完成此项工程需要60天,乙队单独完成此项工程需要90天.
(2)因为需要缩短工期并高效完成工程,所以需两队合作完成,设两队合作这项工程需
y天,根据题意得:
![]()
解得:y=36.
所以需要施工费用36×(8.4+5.6)=504(万元).
因为504>500,所以工程预算的施工费用不够用,需追加预算4万元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
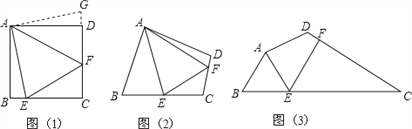
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的 ![]() ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.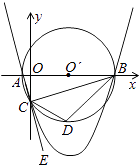
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可完成,需付两组费用共3480元,问:
(1)甲、乙两组工作一天,商店应各付多少元?
(2)已知甲组单独做需12天完成,乙组单独做需24天完成,单独请哪组,商店所付费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在数轴上有A、 B两点,点A表示的数是-6,点B表示的数是9.点P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从点B出发,以每秒3个单位的速度沿数轴负方向运动,当点Q到达点A时,两点同时停止运动,设运动时间为t秒.
(1) AB=____ ;当t=1时,点Q表示的数是___ ;当t=___时,P、Q两点相遇;
(2)如图2,若点M为线段AP的中点,点N为线段BP中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由.若不变,请求出线段MN的长;
(3)如图3,若点M为线段的AP中点,点T为线段BQ中点,则点M表示的数为______;点T表示的数为______;MT=______ (用含t的代数式填空).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题:
(1)统计表中的 m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com