
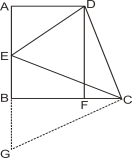
【题目】已知如图,AD∥BC,∠ABC=90o,AB=BC,点E是AB上的点,∠ECD=45o,连接ED,过D作DF⊥BC于F.

(1)若∠BEC=75o,FC=4,求梯形ABCD的周长。(4分)
(2)求证:ED=BE+FC.(6分)
【答案】(1)12![]() +4 (2)通过证明△DEC≌△EGC(AAS),得ED=EG 从而得ED=BE+FC
+4 (2)通过证明△DEC≌△EGC(AAS),得ED=EG 从而得ED=BE+FC
【解析】
试题分析:
(1)∵∠ABC=90o,∠BEC=75o,
∴∠ECB=15o,∵∠ECD=45o,∴∠DCF=60o
在Rt△DFC中:∠DCF=60o,FC=4, ∴DF=4![]() ,DC=8
,DC=8
由题得,四边形ABFD是矩形∴AB=DF=4![]() ,
,
∵AB=BC,∴BC=4![]() ,
,
∴BF=BC-FC=4![]() -4,∴AD=BF=4
-4,∴AD=BF=4![]() -4
-4
∴梯形ABCD的周长为:4![]() +4
+4![]() +8+4
+8+4![]() -4=12
-4=12![]() +4
+4
(2)延长EB至G,使BG=CF,连接CG
∵∠CBG=∠DFC=90o,DF=AB=BC ∴△CBG≌△DFC(SAS)
∴∠CDF=∠GCB,∵∠CDF+∠DCF=90o,∴∠GCB+∠DCF=90o
∵∠DCE=45o,∴∠ECG=45o
∴∠DCE=∠ECG ∴△DEC≌△EGC(AAS),∴ED=EG
∴ED=BE+FC


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com