
 ��֪������L1��y1=x2+6x+5k��������L2��y2=kx2+6kx+5k������k��0��
��֪������L1��y1=x2+6x+5k��������L2��y2=kx2+6kx+5k������k��0������ ��1���ٷֱ��y=0���뼴�ɣ�
�ڸ��ݶ�����ϵ�������жϣ�
�������ߵĶԳ����ǣ�x=-$\frac{b}{2a}$��������㼴�ɣ�
�ܸ��ݡ�=b2-4ac���жϣ�
��2���ɶԳ��Կ�֪�������������ཻ����һ������E���F����������ȣ���F��0��5k���ã�E��-6��5k������EF�͵���0-��-6��=6�������߶�EF=6��
��3������ʵ��k��ʹMN=2EF��
�����䷽���ֱ���M��N�����꣬��������ľ���ã�MN�ij�������MN=2EF�ⷽ�̼��ɣ�
��� �⣺��1���١�������L1��y1=x2+6x+5k������0��5k����������L2��y2=kx2+6kx+5k������0��5k����
��������L1��L2��y�ύ��ͬһ��F��0��5k����
���Ԣٽ�����ȷ��
��������L1��a=1��0���������߿������£�
������L2��k��ȷ��Ϊ�����������������ߵĿ���Ҳ��ȷ����
���Ԣڽ��۲���ȷ��
��������L1���Գ���Ϊֱ�ߣ�x=-$\frac{6}{2��1}$=-3��
������L2���Գ���Ϊֱ�ߣ�x=-$\frac{6k}{2k}$=-3��
��������L1��L2�ĶԳ�����ͬһ��ֱ�ߣ�
���Ԣ۽�����ȷ��
��4��������L1��y1=x2+6x+5k��
��=62-4��1��5k=36-20k��
��k��-1ʱ������0������������L1��x�����������㣬
������L2��y2=kx2+6kx+5k��
��=��6k��2-4��k��5k=16k2��
��k��-1ʱ������0������������L2��x�����������㣬
���Ե�k��-1ʱ��������L1��L2����x�����������㣬
���Ԣܽ�����ȷ��
��˵����ȷ������ǣ��٢ۢܣ�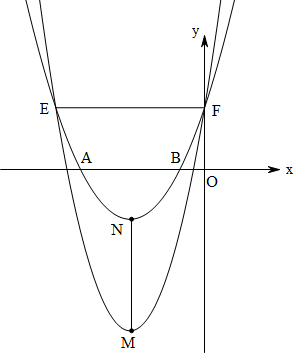
�ʴ�Ϊ���٢ۢܣ�
��2���ɣ�1����֪����F��0��5k����������L1��L2��y��һ�����㣬�����������ཻ����һ������E���F����������ȣ�
��k=1ʱ�����κ���L1��L2�غϣ�
��k��1ʱ��k��ֵ�仯ʱ���߶�EF�ij�����仯��
�����ǣ���������L1��L2�ĶԳ�����ͬһ��ֱ�ߣ�ֱ��x=-3����F��0��5k����
���F����ֱ��x=-3�ԳƵĵ�E������ΪE��-6��5k������EF�͵���0-��-6��=6��
�����߶�EF=6��
��3������ʵ��k��ʹMN=2EF��
y1=x2+6x+5k=��x+3��2-9+5k��y2=kx2+6kx+5k=k��x+3��2-4k��
��������L1������M��-3��-9+5k����
������L2������N��-3��-4k����
������ã�NM=|-4k-��5k-9��|=2��6��
��ã�k1=$\frac{7}{3}$��k2=-$\frac{1}{3}$��
���� �����Ƕ��κ������ۺ��⣬�����˶��κ��������ʡ������䷽����������ꡢ�Գ��ᡢ����ľ��롢һԪ���η��̡������б�ʽ�����������ν�ϵ�˼�룬����ͼ�������⣻�������ն��κ����ĶԳ����DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
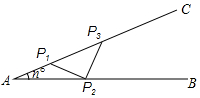 ��ͼ�ּ��У���A=14�㣬���κ��ϵȳ��ĸ���P1P2��P2P3���������ӹ̸ּܣ������ĸ�������ܺ�������������
��ͼ�ּ��У���A=14�㣬���κ��ϵȳ��ĸ���P1P2��P2P3���������ӹ̸ּܣ������ĸ�������ܺ�������������| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
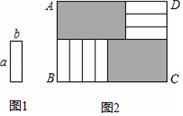 ������ͼ1�ij�Ϊa����Ϊb��a��b����С������ֽƬ����ͼ2�ķ�ʽ���ص��ط��ڳ�����ABCD�ڣ�δ�����ǵIJ��֣����������Σ�����Ӱ���֣������Ͻ������½ǵ���Ӱ���ֵ�����IJ�ΪS=S1-S2����BC�ij��ȱ仯ʱ������ͬ���ķ��÷�ʽ��Sʼ�ձ��ֲ��䣬��a��b����Ĺ�ϵʽ��a=3b��
������ͼ1�ij�Ϊa����Ϊb��a��b����С������ֽƬ����ͼ2�ķ�ʽ���ص��ط��ڳ�����ABCD�ڣ�δ�����ǵIJ��֣����������Σ�����Ӱ���֣������Ͻ������½ǵ���Ӱ���ֵ�����IJ�ΪS=S1-S2����BC�ij��ȱ仯ʱ������ͬ���ķ��÷�ʽ��Sʼ�ձ��ֲ��䣬��a��b����Ĺ�ϵʽ��a=3b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ѧУ�Ķ��� | B�� | �ڶ��Ϸ���800�״� | ||
| C�� | ��ѧУ800�״� | D�� | ��ѧУ���Ϸ���800�״� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
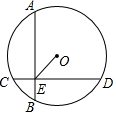 ��ͼ����O��ֱ��Ϊ10��������AB��CD������ΪE����AB=CD=8����OE=3$\sqrt{2}$��
��ͼ����O��ֱ��Ϊ10��������AB��CD������ΪE����AB=CD=8����OE=3$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������61 | B�� | ��λ��Ϊ57 | C�� | ������39 | D�� | ƽ����Ϊ58 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������� | B�� | �������� | C�� | �ڶ����� | D�� | ��һ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3$\sqrt{2}$-$\sqrt{2}$=3 | B�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C�� | 2$\sqrt{3}$��3$\sqrt{3}$=6$\sqrt{3}$ | D�� | $\sqrt{121��4}$=$\sqrt{121}$��$\sqrt{4}$=$\frac{11}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com