
【题目】如下几个图形是五角星和它的变形.

(1)图甲是一个五角星 ABCDE,则∠A+∠B+∠C+∠D+∠E 的度数为 ;(不必 写过程)
(2)如图乙,如果点 B 向右移动到 AC 上时,则∠A+∠EBD+∠C+∠D+∠E 度数为 ;(不必写过程)
(3)如图丙,点 B 向右移动到 AC 的另一侧时,(1)的结论成立吗?为什么?
(4)如图丁,点 B,E 移动到∠CAD 的内部时,结论又如何?(不必写过程)
【答案】(1)180°;(2)180°;(3)成立;(4)∠A+∠B+∠C+∠D+∠E=180°..
【解析】
(1)由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2;(2)由三角形的外角性质,由∠A+∠D=∠1,得∠1+∠DBE+∠C+∠E=180°;(3)由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,根据三角形内角和定理可得;(4)延长CE与AD相交,由三角形的外角性质,∠A+∠C=∠1,∠B+∠E=∠2,根据三角形内角和定理可得.
(1)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图,由三角形的外角性质,∠A+∠D=∠1,
∵∠1+∠DBE+∠C+∠E=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°;
(3)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(4)如图,延长CE与AD相交,由三角形的外角性质,∠A+∠C=∠1,∠B+∠E=∠2,
∵∠1+∠2+∠D=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)9x2-100=0 (2)x(x-1)=2(x-1)
(3)(x+2)(x+3)=20 (4)3x2-4x-1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
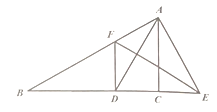
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 平分线,
平分线,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 延长线于点
延长线于点![]() .求证:
.求证:![]() .
.
证明:∵![]() 平分
平分![]()
∴![]()
![]() (角平分线的定义)
(角平分线的定义)
∵![]() 垂直平分
垂直平分![]()
∴ ![]() (线段垂直平分线上的点到线段两个端点距离相等)
(线段垂直平分线上的点到线段两个端点距离相等)
∴![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
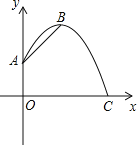
【题目】一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成45°角,水流最高点B比喷头A高2米.
(1)求水流落地点C到O点的距离;
(2)若水流的水平位移s(米)(抛物线上两对称点之间的距离)与水流的运动时间(t秒)之间的函数关系为t= 0.8s,求共有几秒钟,水流高度不低于2米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新合作超市最近进了一批玩具,进价每个15元,今天共卖山20个,实际卖出的价格以每个18元为标准,超过的记为正,不足的记为负,记录如下:
实际每个售出价格与标准的差值(单位:元) | +3 | -1 | +2 | +1 |
个数 | 5 | 4 | 6 | 5 |
(1)这个超市今天卖出玩具的平均价格是多少?
(2)这个超市今天卖出的玩具赚了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=![]() ,BE=
,BE=![]() .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O的半径为5cm,AB,CD是⊙O的两条弦,AB‖CD,AB=8,CD=6,AB和CD之间的距离是___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF.

(1)求证:四边形AECF是平行四边形.
(2)如果四边形ABCD是菱形,求证:四边形AECF也是菱形.
(3)如果四边形ABCD是矩形,请判断四边形AECF的形状,不必写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com