
分析 根据题意得出m<0,n<0,再根据二次根式的乘除法法则和二次根式的性质进行计算,即可得出结论.
解答 解:∵mn>0,m+n<0,
∴m<0,n<0,
∴$\sqrt{\frac{m}{n}}$•$\sqrt{\frac{n}{m}}$=$\sqrt{\frac{m}{n}•\frac{n}{m}}$=1,①正确;
②$\sqrt{\frac{m}{n}}$=$\frac{\sqrt{m}}{\sqrt{n}}$错误;
$\sqrt{mn}$•$\sqrt{\frac{m}{n}}$=$\sqrt{{m}^{2}}$=-m,③错误;
故答案为:①.
点评 本题考查了二次根式的乘除法法则、二次根式的性质;根据题意得出m<0,n<0是解决问题的关键.


科目:初中数学 来源: 题型:解答题
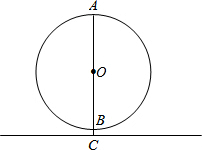 如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,
如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
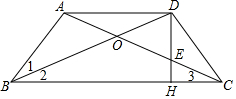 如图,已知四边形ABCD中,AC与BD相交于点O,OA=OD,∠1=∠2=∠3,∠BAC=90°,DH⊥BC于H,DH交AC于E.
如图,已知四边形ABCD中,AC与BD相交于点O,OA=OD,∠1=∠2=∠3,∠BAC=90°,DH⊥BC于H,DH交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com