
����Ŀ����֪����ͼ������������y��ax��ͼ���뷴��������y��![]() ��ͼ���ڵ�A��3��2��
��ͼ���ڵ�A��3��2��
��1����ȷ�����������������ͷ����������ı���ʽ��
��2������ͼ��ش��ڵ�һ�����ڣ���xȡ��ֵʱ��������������ֵ����������������ֵ��
��3����M��m��n���Ƿ���������ͼ���ϵ�һ���㣬����0��m��3������M��ֱ��MB��x�ᣬ��y���ڵ�B������A��ֱ��AC��y�ύx���ڵ�C����ֱ��MB�ڵ�D�����ı���OADM�����Ϊ6ʱ�����ж��߶�BM��DM�Ĵ�С��ϵ����˵�����ɣ�

���𰸡�(1) y��![]() x��y��
x��y��![]() ��(2)0��x��3��(3)BM��DM��
��(2)0��x��3��(3)BM��DM��
�������������������1����A������ֱ��������������ʽ�����a��k��ֵ��������������Ľ���ʽ����2���ɷ�����������ͼ��������������ͼ����Ϸ�����ö�Ӧ��x��ȡֵ��Χ����3����M�������ɱ�ʾ����OCDB���������OBM��������Ӷ��ɱ�ʾ���ı���OADM��������ɵõ����̣������M������꣬�Ӷ���֤�����ۣ�
�����������1��������������y=ax��ͼ���뷴��������y=![]() ��ͼ���ڵ�A��3��2������2=3a��2=
��ͼ���ڵ�A��3��2������2=3a��2=![]() �����a=
�����a=![]() ��k=6������������������ʽΪy=
��k=6������������������ʽΪy=![]() x����������������ʽΪy=
x����������������ʽΪy=![]() ����2����ͼ���֪��������ͼ����ֱ��CD�����ʱ��������������ͼ��������������ͼ����Ϸ�����A��3��2��������0��x��3ʱ��������������ֵ����������������ֵ����3���������֪�ı���OCDBΪ���Σ���M��m��n����A��3��2������OB=n��BM=m��OC=3��AC=2����S����OCBD=OCOB=3n��S��OBM=
����2����ͼ���֪��������ͼ����ֱ��CD�����ʱ��������������ͼ��������������ͼ����Ϸ�����A��3��2��������0��x��3ʱ��������������ֵ����������������ֵ����3���������֪�ı���OCDBΪ���Σ���M��m��n����A��3��2������OB=n��BM=m��OC=3��AC=2����S����OCBD=OCOB=3n��S��OBM=![]() OBBM=
OBBM=![]() mn��S��OCA=
mn��S��OCA=![]() OCAC=3����S�ı���OADM=S����OCBD��S��OBM��S��OCA=3n��
OCAC=3����S�ı���OADM=S����OCBD��S��OBM��S��OCA=3n��![]() mn��3�����ı���OADM�����Ϊ6ʱ������3n��
mn��3�����ı���OADM�����Ϊ6ʱ������3n��![]() mn��3=6������M���ڷ���������ͼ���ϣ���mn=6����3n=12�����n=4����m=
mn��3=6������M���ڷ���������ͼ���ϣ���mn=6����3n=12�����n=4����m=![]() ����BD=OC=3����MΪBD�е㣬��BM=DM��
����BD=OC=3����MΪBD�е㣬��BM=DM��


 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
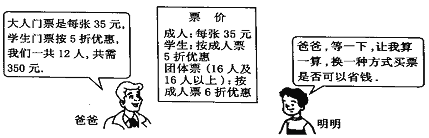
����Ŀ�������ڼ䣬���꼶(1)���������������ͬѧ��ҳ�һͬ��ij�����棬��ͼ�ǹ�����Ʊʱ�����������ְֵĶԻ����Ը���ͼ�е���Ϣ������������⣺
(1)��������һ��ȥ�˼�������?����ѧ����
(2)�������������һ�㣬�����ַ�ʽ��Ʊ��ʡǮ?
(3)����Ʊ�������������꼶(2)�����С�ε�8��ѧ�������ǵ�12���ҳ���20��Ҳ����Ʊ������Ϊ������Ƴ���ʡǮ�Ĺ�Ʊ�������������ʱ�Ĺ�Ʊ���á�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵ�ֱ��������ƴ����ͼ�Σ���ƽ���ı��Σ������Σ������Σ��������Σ������������Σ����ȱ������Σ�����ƴ�ɵ�ͼ���� �� ��
A���٢ܢ� B���ڢݢ� C���٢ڢ� D���٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���һ�麬��45���ǵ�ֱ�����ǰ���ͼ���ã�ֱ�Ƕ���C������Ϊ��1��0��������A������Ϊ��0��2��������Bǡ�����ڵ�һ����˫�����ϣ��ֽ�ֱ�����ǰ���x��������ƽ�ƣ�������Aǡ�����ڸ�˫������ʱֹͣ�˶������ʱ��C�Ķ�Ӧ��C��������Ϊ�� ��
A. ��![]() ��0�� B. ��2��0�� C. ��
��0�� B. ��2��0�� C. ��![]() ��0�� D. ��3��0��
��0�� D. ��3��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ǿѧ�����������ʣ�ijУ��ֳ����ȫԱ���������������ڽ������ܲ��ԣ����潫ij��ѧ��������Զ�ɼ�����ȷ��0��1m�����������ֳ�5�飨����ֵ������ֵ����1.60��1.80��1.80��2.00��2.00��2.20��2.20��2.40��2.40��2.60����֪ǰ4��С���Ƶ�ʷֱ���0.05��0.15��0.30��0.35�������С���Ƶ����9��
��1���ð�μ�������Ե������Ƕ����ˣ�
��2���뻭��Ƶ���ֲ�ֱ��ͼ��
��3���ɼ���2.00�����ϣ���2.00�ף�Ϊ�ϸ���ð�ɼ��ĺϸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��1��2����B��3��1����C����2����1����
��1����ͼ��������ABC����y��ԳƵ���A1B1C1��
��2��д��A1��B1��C1�����꣬A1�� ��B1��������C1����������ֱ��д���𰸣�
��3����A1B1C1�����Ϊ������ ����������ֱ��д���𰸣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C��D�ֱ���������Բ�ϣ������A��B�غϣ���AD��BD�ij��ֱ��ǹ���x�ķ���![]() ��0������ʵ������
��0������ʵ������
��1����m��ֵ��
��2������CD����̽����AC��BC��CD����֮��ĵ�����ϵ����˵�����ɣ�
��3����CD��![]() ����AC��BC�ij���
����AC��BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
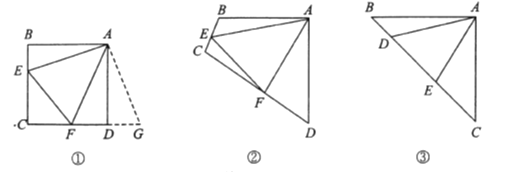
����Ŀ��ͨ��������롢������չ�о�������Ŀ���ɴﵽ��һ��֪һ���Ŀ�ģ�������һ��������
ԭ������ͼ������![]() �ֱ���������
�ֱ���������![]() �ı�
�ı�![]() ����
���� ![]() ������
������![]() ����
����![]() ����˵�����ɣ�
����˵�����ɣ�
��1��˼·����
��Ϊ![]() ������
������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת90����
��ʱ����ת90����![]() ����ʹ
����ʹ![]() ��
��![]() �غϣ���Ϊ
�غϣ���Ϊ![]() ������
������![]() ����
����![]() ���ߣ�
���ߣ�
���� ����֤![]() ����
����![]() .��֤����
.��֤����
��2���������
��ͼ�����ı���![]() ����
���� ![]() ��
�� ![]() ����
����![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ����
���� ![]() .��
.��![]() ������ֱ������
������ֱ������![]() ��
��![]() ���������ϵʱ��
���������ϵʱ�� ![]() ��Ȼ��������֤����
��Ȼ��������֤����
��3��������չ
��ͼ������![]() ����
���� ![]() ����
����![]() ���ڱ�
���ڱ�![]() ������
������![]() .����
.����![]() Ӧ����ĵ�����ϵ����д��֤�����̣�
Ӧ����ĵ�����ϵ����д��֤�����̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com