
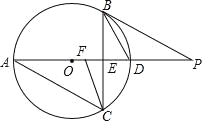
【题目】如图,已知△ABC内接于⊙O,直径AD⊥BC于E,点F是OE的中点,且BD∥CF.
(1)若BD=3![]() ,求BC的长.
,求BC的长.
(2)若BD平分∠CBP,求证:ABBD=BPAF.
【答案】(1)BC=2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由直径AD⊥BC,根据垂径定理得到E为BC中点,又BD与CF平行,得到两对内错角相等,从而利用“AAS”得到三角形BDE与三角形CFE全等,根据全等三角形的对应边相等得到DE=EF,设ED=EF=x,由已知F为OE中点,得到OE=2EF=2x,OD=OA=3x,则AD=6x,再由直径AB所对的圆周角为直角得到∠ABD=90°,又根据垂直定义得到∠AEB=90°,故两个角相等,再根据∠BED为公共角,利用两对对应角相等的两三角形相似得到△ABD∽△BED,由相似得比例列出关于x的方程,求出方程的解即可得到x的值,即可求出BD和DE,在直角三角形BDE中,利用勾股定理求出BE的长,进而求出BC的长;
(2)连接BF,根据AB为圆的直径,得到其所对的圆周角为直角,根据直角三角形两锐角互余得到∠BAD+∠ADB=90°又根据AD与BC垂直根据垂直定义得到一个直角,同理可得∠DBE+∠ADB=90°,根据同角的余角相等得到∠BAD=∠DBE,根据角平分线定义得到∠PBD=∠DBE,利用等量代换得到∠BAD=∠PBD,由(1)可知BE垂直平分FD,故BF=BD,根据“等边对等角”得到∠BFD=∠BDF,再根据等角的邻补角相等得到一对角相等,由两对对应角相等的两三角形相似,得到△ABF∽△BPD,由相似得比例变形后得证.
解:(1)∵直径AD⊥BC于E,
由垂径定理得:BE=CE,
又∵BD∥CF,
∴∠ECF=∠EBD,∠EFC=∠EDB,
∴△BED≌△CEF,
∴DE=EF,
设DE=EF=x,
又∵点F是OE的中点,
∴OE=2EF=2x,OD=OA=3x,AD=6x,
∵AD是⊙O直径,
∴∠ABD=90°,
又AD⊥BC,∴∠AEB=90°,
∴∠ABD=∠AEB,又∠BDE=∠BDE,
∴△ABD∽△BED,
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,
,
在直角三角形BDE中,
根据勾股定理得:BE=![]() ,
,
则BC=2BE=2![]() ;
;

(2)连接BF,AB,
∵AD是⊙O直径,
∴∠ABD=90°,
∴∠BAD+∠ADB=90°
又AD⊥BC,∴∠AEB=90°,
∴∠DBE+∠ADB=90°,
∴∠BAD=∠DBE,
又∵BD平分∠CBP,
∴∠PBD=∠DBE,
∴∠BAD=∠PBD,
由(1)可知:DE=EF,且AD⊥BC,
∴BE是DF的垂直平分线,
∴BF=BD,
∴∠BFD=∠BDF,
∴∠AFB=∠BDP,
∴△ABF∽△BPD,
∴![]() ,即ABBD=BPAF.
,即ABBD=BPAF.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
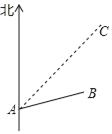
【题目】如图,台风中心位于点A,并沿东北方向AC移动,已知台风移动的速度为50千米/时,受影响区域的半径为130千米,B市位于点A的北偏东75°方向上,距离A点240千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
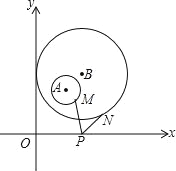
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
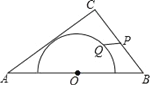
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.

(1)求抛物线的解析式;
(2)当0<t≤8时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要加工甲、乙、丙三种型号机械配件共120个,安排20个工人刚好一天加工完成,每人只加工一种配件,设加工甲种配件的人数为x,加工乙种配件的人数为y,根据下表提供的信息,解答下列问题:
配件种类 | 甲 | 乙 | 丙 |
每人每天加工配件的数量 | 8 | 6 | 5 |
每个配件获利 | 15 | 14 | 8 |
![]() 求y与x之间的关系.
求y与x之间的关系.
![]() 若这些机械配件共获利1420元,请求出加工甲、乙、丙三种型号配件的人数分别是多少人?
若这些机械配件共获利1420元,请求出加工甲、乙、丙三种型号配件的人数分别是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,产量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足函数关系式
满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材的市场需求量
,从市场反馈的信息发现,该半成品食材的市场需求量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足一次函数关系,如下表:
满足一次函数关系,如下表:
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元![]() 千克且不高于10元
千克且不高于10元![]() 千克
千克
![]() 求q与x的函数关系式;
求q与x的函数关系式;
![]() 当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
![]() 当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃
当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃![]() 若该半成品食材的成本是2元
若该半成品食材的成本是2元![]() 千克.
千克.
![]() 求厂家获得的利润
求厂家获得的利润![]() 百元
百元![]() 与销售价格x的函数关系式;
与销售价格x的函数关系式;
![]() 当厂家获得的利润
当厂家获得的利润![]() 百元
百元![]() 随销售价格x的上涨而增加时,直接写出x的取值范围
随销售价格x的上涨而增加时,直接写出x的取值范围![]() 利润
利润![]() 售价
售价![]() 成本
成本![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com