
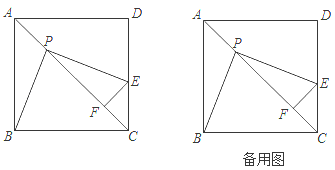
【题目】已知边长为1的正方形ABCD中,P是对角线AC上的一个动点(与点A. C不重合),过点P作PE⊥PB,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F,当点E落在线段CD上时(如图),
(1)求证:PB=PE;
(2)在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;
【答案】(1)见解析;(2)![]()
【解析】
(1)过点P作PG⊥BC于G,过点P作PH⊥DC于H,如图1.要证PB=PE,只需证到△PGB≌△PHE即可;(2)连接BD,如图2.易证△BOP≌△PFE,则有BO=PF,只需求出BO的长即可.
(1)①证明:过点P作PG⊥BC于G,过点P作PH⊥DC于H,如图1.
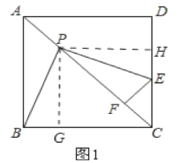
∵四边形ABCD是正方形,PG⊥BC,PH⊥DC,
∴∠GPC=∠ACB=∠ACD=∠HPC=45°.
∴PG=PH,∠GPH=∠PGB=∠PHE=90°.
∵PE⊥PB即∠BPE=90°,
∴∠BPG=90°∠GPE=∠EPH.
在△PGB和△PHE中,
 .
.
∴△PGB≌△PHE(ASA),
∴PB=PE.
②连接BD,如图2.

∵四边形ABCD是正方形,∴∠BOP=90°.
∵PE⊥PB即∠BPE=90°,
∴∠PBO=90∠BPO=∠EPF.
∵EF⊥PC即∠PFE=90°,
∴∠BOP=∠PFE.
在△BOP和△PFE中,
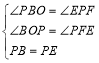 ,
,
∴△BOP≌△PFE(AAS),
∴BO=PF.
∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90,
∴BC=![]() OB.
OB.
∵BC=1,∴OB=![]() ,
,
∴PF=![]() .
.
∴点PP在运动过程中,PF的长度不变,值为![]() .
.


科目:初中数学 来源: 题型:
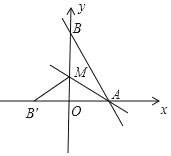
【题目】已知直线y=﹣![]() x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的函数解析式是( )
x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的函数解析式是( )
A. y=﹣![]() x+8 B. y=﹣
x+8 B. y=﹣![]() x+8 C. y=﹣
x+8 C. y=﹣![]() x+3 D. y=﹣
x+3 D. y=﹣![]() x+3
x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传球三次.
(1)请利用树状图列举出三次传球的所有可能情况;
(2)求三次传球后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.
(1)求证:AF=CE;
(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论
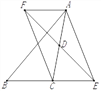
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于![]() 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )![]()
A. 29
B. 28
C. 30
D. 31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y1=![]() (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
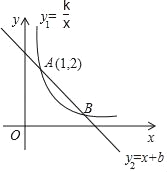
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() 长为3,
长为3,![]() 长为6,点
长为6,点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 以每秒1个单位的速度运动,同时点
以每秒1个单位的速度运动,同时点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 以每秒2个单位的速度运动(当一个点到达终点时另一个点也随之停止运动).若运动的时间为
以每秒2个单位的速度运动(当一个点到达终点时另一个点也随之停止运动).若运动的时间为![]() 秒,则三角形
秒,则三角形![]() 的面积为______(用含
的面积为______(用含![]() 的式子表示).
的式子表示).
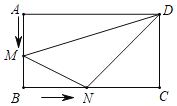
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com