
| 判别式△=b2-4ac | △>0 | △=0 | △<0 |
| 二次函数y=ax2+bx+c(a>0)的图象 | 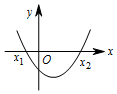 |  | 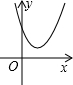 |
| 一元二次方程y=ax2+bx+c(a>0)的根 | 有两个不相等的实数根 x1=$\frac{-b+\sqrt{△}}{2a}$,x2=$\frac{-b-\sqrt{△}}{2a}$(x1<x2) | 有两个相等的实数根 x1=x2=-$\frac{b}{2a}$ | 无实数根 |
| 使y>0的x的取值范围 | x<x1或x>x2 | x≠-$\frac{b}{2a}$ | 全体实数 |
| 不等式ax2+bx+c>0(a>0)的解集 | 无解 | x≠-$\frac{b}{2a}$ | 无解 |
分析 解一元二次不等式ax2+bx+c>0(a≠0)实质上就是求抛物线图象在x轴上方时,自变量的取值范围,抛物线开口方向及与x轴的交点情况就决定了函数值什么情况下大于0,即ax2+bx+c>0.
解答 解:(1)
| 判别式 △=b2-4ac | △>0 | △=0 | △<0 |
| 二次函数 y=ax2+bx+c(a>0)的图象 |  |  | |
| 一元二次方程 ax2+bx+c=0(a>0)的根 | |||
| 使y>0的x的取值范围 | x≠-$\frac{b}{2a}$ | 全体实数 | |
| 不等式ax2+bx+c>0(a>0)的解集 | x<x1或x>x2 | 全体实数 | |
| 不等式ax2+bx+c<0(a>0)的解集 | x1<x<x2 | 无解 | 无解 |
点评 本题主要考查了二次函数的性质与一元二次不等式之间的关系,以及图象与x轴的位置关系.这些性质和规律要求掌握.


科目:初中数学 来源: 题型:选择题
 实数a,b在数轴上的位置如图所示,则下列结论中:①ab<0;②a<|b|;③a+b<0;④|b|=b;⑤|a-b|=b-a,正确的有( )
实数a,b在数轴上的位置如图所示,则下列结论中:①ab<0;②a<|b|;③a+b<0;④|b|=b;⑤|a-b|=b-a,正确的有( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com