
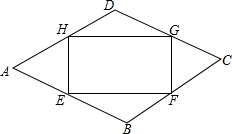
 如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH.其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°
如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH.其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°分析 (1)根据菱形的性质得△AHE是等边三角形,即HE=(a-x)米,过点P作DP⊥HG于点P,则HG=2HP=2DHsin∠HDP=$\sqrt{3}$x米,由矩形面积公式可得;
(2)将a=100代入上式,配方成顶点式可得其最值情况;
(3)将(1)中函数解析式配方后,根据其最值可得关于a的方程,解方程即可得.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=AD=a米,
∵BE=BF=DH=DG=x米,∠A=60°
∴AE=AH=(a-x)米,∠ADC=120°,
∴△AHE是等边三角形,即HE=(a-x)米,
如图,过点P作DP⊥HG于点P,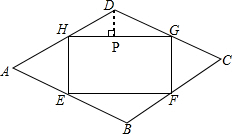
∴HG=2HP,∠HDP=$\frac{1}{2}$∠ADC=60°,
则HG=2HP=2DHsin∠HDP=2x×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$x米,
∴S=$\sqrt{3}$x(a-x)=-$\sqrt{3}$x2+$\sqrt{3}$ax (0<x<a);
(2)当a=100时,S=-$\sqrt{3}$x2+100$\sqrt{3}$x=-$\sqrt{3}$(x-50)2+2500$\sqrt{3}$,
∴当x=50时,S取得最大值,最大值为2500$\sqrt{3}$.
(3)S=-$\sqrt{3}$x2+$\sqrt{3}$ax=-$\sqrt{3}$(x-$\frac{a}{2}$)2+$\frac{\sqrt{3}}{4}$a2,
根据题意,得:$\frac{\sqrt{3}}{4}$a2=10000$\sqrt{3}$,
解得:a=200或a=-200(舍),
故a至少需要200米.
点评 本题主要考查二次函数的实际应用,根据菱形的性质及等腰三角形性质、三角函数表示出矩形的长宽是求得函数解析式的前提,熟练掌握二次函数的性质是求函数最值的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com