
【题目】如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积 . 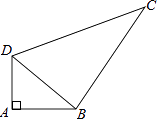
【答案】36
【解析】解:在△ABD中, ∵∠A=90°,AD=3,AB=4,
∴BD= ![]() =5,
=5,
S△ABD= ![]() ABAD=
ABAD= ![]() ×4×3=6,
×4×3=6,
在△BCD中,
∵BC=12,CD=13,BD=5,
∴BD2+BC2=CD2 ,
∴△CBD是直角三角形,
∴S△CBD= ![]() BCBD=
BCBD= ![]() ×12×5=30.
×12×5=30.
∴四边形ABCD的面积=S△ABD+S△BCD=6+30=36.
所以答案是:36.
【考点精析】根据题目的已知条件,利用勾股定理的概念和勾股定理的逆定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A. 70° B. 70°或86° C. 86° D. 30°或38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE. 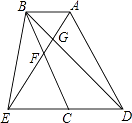
(1)求证:△AFB≌△EFG;
(2)判断CF与AD的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
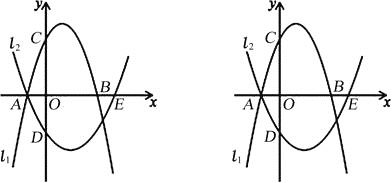
【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com