
【题目】如图,四边形ABCD中,∠ABC、∠ADC的平分线分別交CD、AB上点E、F.

(1)若∠ABC=∠ADC,求征:∠ADF=∠ABE;
(2)如图,若∠A与∠C互朴,试探究∠ADF与∠ABE之同的数量夫系,并说明理由;

(3)如图,在(2)的条件下,当DA⊥AB时,试探究BE与DF的位置关系,并说明理由.

【答案】(1)见解析;(2)∠ADF+∠ABE=90°,见解析;(3)DF∥BE,见解析.
【解析】
(1)由角平分线知∠ADF=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC,结合∠ABC=∠ADC可得答案;
∠ABC,结合∠ABC=∠ADC可得答案;
(2)由∠A+∠C=180°知∠ADC+∠ABC=180°,结合∠ADF=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC,得∠ADF+∠ABE=
∠ABC,得∠ADF+∠ABE=![]() (∠ADC+∠ABC)可得答案;
(∠ADC+∠ABC)可得答案;
(3)根据四边形内角和得到∠ABC+∠ADC=180°,再根据角平分线定义得到∠ABE=![]() ∠ABC,∠ADF=
∠ABC,∠ADF=![]() ∠ADC,则∠ABE+∠ADF=90°,加上∠AFD+∠ADF=90°,利用等角的余角相等得∠AFD=∠ABE,然后根据平行线的判定定理得到DF∥BE.
∠ADC,则∠ABE+∠ADF=90°,加上∠AFD+∠ADF=90°,利用等角的余角相等得∠AFD=∠ABE,然后根据平行线的判定定理得到DF∥BE.
解:(1)∵DF平分∠ADC,BE平分∠ABC,
∴∠ADF=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC,
∠ABC,
又∠ABC=∠ADC,
∴∠ADF=∠ABE;
(2)∵∠A+∠C=180°,
∴∠ADC+∠ABC=180°,
又∠ADF=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC,
∠ABC,
∴∠ADF+∠ABE=![]() (∠ADC+∠ABC)=90°;
(∠ADC+∠ABC)=90°;
(3)DF与BE平行.
理由如下:
∵DA⊥AB,
∴在四边形ABCD中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.
∴∠ABE=![]() ∠ABC,∠ADF=
∠ABC,∠ADF=![]() ∠ADC,
∠ADC,
∴∠ABE+∠ADF=90°,
而∠AFD+∠ADF=90°,
∴∠AFD=∠ABE,
∴DF∥BE.
故答案为:(1)见解析;(2)∠ADF+∠ABE=90°,见解析;(3)DF∥BE,见解析.


科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,C为BD上一点,使得CA=CD,过点C作CE∥AD交AB于点E,过点D作DF⊥AD交AC的处长线于点F.
(1)若CD=3,求AF的长;
(2)若∠B=30°,∠ADC=40°,求证:AC=EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知点A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
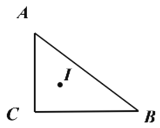
【题目】在Rt△ABC中,∠C=90°,AB=10,BC=8,AC=6.点I为△ABC三条角平分线的交点,则点I到边AB的距离为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级261位学生参加期末考试,某班35位学生的语文成绩、数学成绩与总成绩在全年级中排名情况如图1和图2所示,甲、乙、丙为该班三位学生.

从这次考试成绩看,①在甲、乙两人中,总成绩名次靠前的学生是______;
②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是______.
你选择的理由是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在平面直角坐标系xOy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动,设点P、点Q的运动时间为t(s).
(1)当t=1 s时,求经过点O,P,A三点的抛物线的解析式;
(2)当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;
(3)连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com