
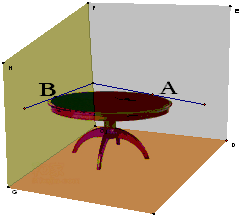
 马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的| 1 | 5 |
 |
| AmB |
 |
| AB |
| 1 |
| 5 |
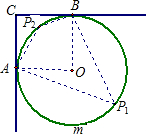 解:(1)设圆桌所在圆的圆心为O,过切点的切线AC、BC交于C,p为异于A、B的圆周上的任意一点.
解:(1)设圆桌所在圆的圆心为O,过切点的切线AC、BC交于C,p为异于A、B的圆周上的任意一点. |
| AmB |
 |
| AB |
| 1 |
| 5 |
| 36 |
| -2 |


科目:初中数学 来源: 题型:
.(本题15分)
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的![]() ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数
(2)请你求出马田同学作业中的
那条抛物线的对称轴方程.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省德州市育英中学初三中考模拟考试数学卷 题型:解答题
.(本题15分)
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的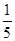 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: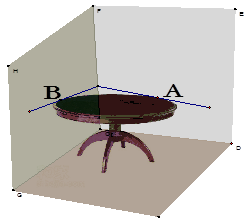 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数
(2)请你求出马田同学作业中的
那条抛物线的对称轴方程.
查看答案和解析>>
科目:初中数学 来源:2012年云南省中考数学模拟试卷(二)(解析版) 题型:解答题
 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
查看答案和解析>>
科目:初中数学 来源:2012年江苏省连云港市灌南县灌河中学中考数学模拟试卷(一)(解析版) 题型:解答题
 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com