
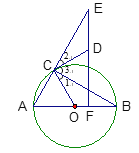
【题目】如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.
(1)∠E= °;
(2)△DCE是什么特殊三角形?请说明理由;
(3)当⊙O的半径为1,BF=![]() 时,求证△DCE≌△OCB.
时,求证△DCE≌△OCB.

【答案】(1)30°; (2)△DCE为等腰三角形; 理由见解析;(3)证明见解析
【解析】【试题分析】(1)AB为⊙O的直径,则
![]() ,因为∠ABC=30°,则
,因为∠ABC=30°,则![]() ,因为ED⊥AB,则∠E=30°
,因为ED⊥AB,则∠E=30°
(2)△DCE为等腰三角形.理由:∠1=30°,根据同角的余角相等,得∠2=30°=∠E
得△DCE为等腰三角形.
(3)由(2)得△DCE∽△OCB,在Rt△ABC中, 求得BC=![]() =
=![]() . AF=AB-BF=2-
. AF=AB-BF=2-![]() =
=![]() ,在Rt△AEF中,
,在Rt△AEF中,
则AE=2AF=1+![]() ,CE=AE-AC=1+
,CE=AE-AC=1+![]() -1=
-1=![]() .
.
CE=BC=![]() ,△DCE≌△OCB得证。
,△DCE≌△OCB得证。
【试题解析】
(1)AB为⊙O的直径,则
![]() ,因为∠ABC=30°,则
,因为∠ABC=30°,则![]() ,因为ED⊥AB,则∠E=30°
,因为ED⊥AB,则∠E=30°
(2)△DCE为等腰三角形.
∵CD是⊙O的切线,∴∠OCD=90°.
即∠1+∠3=90°(如图).
∵AB为⊙O的直径,∴∠ACB=90°,
∴∠ECB=90°,即∠2+∠3=90°,
∴∠1=∠2.∵∠B=30°,∴∠A=60°;
∵OC=OB,∴∠1=∠B=30°,∴∠2=30°.
∵ED⊥AB于点F,∴∠E=90°-∠A=30°,
∴∠E=∠2,故△DCE的等腰三角形;
(3)证明:在Rt△ABC中,∵∠B=30°,
∴AC=![]() AB=
AB=![]() ×2=1.
×2=1.
∴BC=![]() =
=![]() .
.
AF=AB-BF=2-![]() =
=![]()
在Rt△AEF中,∵∠E=30°,
∴AE=2AF=1+![]() ,
,
∴CE=AE-AC=1+![]() -1=
-1=![]() .在△DCE和△OCB中,
.在△DCE和△OCB中,
∵∠E=∠2=∠B=∠1=30°,CE=BC=![]() ,∴△DCE≌△OCB.
,∴△DCE≌△OCB.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.

【答案】(1)画图见解析;(2)A(﹣2,0)B(0,4);(3)4;(4)x<﹣2.
【解析】试题分析:(1)求得一次函数y=2x+4与x轴、y轴的交点坐标,利用两点确定一条直线就可以画出函数图象;(2)由(1)即可得结论;(3)通过交点坐标根据三角形的面积公式即可求出面积;(4)观察函数图象与x轴的交点就可以得出结论.
试题解析:(1)当x=0时y=4,当y=0时,x=﹣2,则图象如图所示

(2)由上题可知A(﹣2,0)B(0,4),
(3)S△AOB=![]() ×2×4=4,
×2×4=4,
(4)x<﹣2.
考点:一次函数图象与系数的关系;一次函数的图象.
【题型】解答题
【结束】
21
【题目】在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:

(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四个等级,并绘制成下面的频数分布表(表一)和扇形统计图(图①)。
表一
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | 12 | 0.24 | |
B | 8分 |
|
|
7分 | 8 | 0.16 | |
C | 6分 |
|
|
5分 | 1 | 0.02 | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |

(1)求出![]() 、
、![]() 的值,直接写出
的值,直接写出![]() 、
、![]() 的值;
的值;
(2)求表示得分为C等级的扇形的圆心角的度数;
(3)如果该校九年级共有男生250名,试估计这250名男生中成绩达到A等级的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
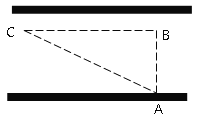
【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于A、B两点(A在B的左侧),且A、B两点的横坐标是方程
轴交于A、B两点(A在B的左侧),且A、B两点的横坐标是方程![]() -12=0的两个根.抛物线与
-12=0的两个根.抛物线与![]() 轴的正半轴交于点C,且OC=AB.
轴的正半轴交于点C,且OC=AB.
(1)求A、B、C三点的坐标;
(2)求此抛物线的解析式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为![]() ,△CEF的面积为S,求S与
,△CEF的面积为S,求S与![]() 之间的函数关系式;
之间的函数关系式;
(4)对于(3),试说明S是否存在最大值或最小值,若存在,请求出此值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一天,龟、兔进行了600米赛跑,如图表示龟兔赛跑的路程s(米)与时间t(分钟)的关系(兔子睡觉前后速度保持不变),根据图象回答以下问题:
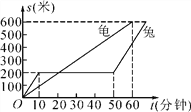
(1)赛跑中,兔子共睡了多少时间?
(2)赛跑开始后,乌龟在第几分钟时从睡觉的兔子旁经过?
(3)兔子跑到终点时,乌龟已经到了多长时间?并求兔子赛跑的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在选拔2016年第十三届全国冬季运动会速滑运动员时,教练打算根据平时训练成绩,从运动员甲和乙种挑选1名成绩稳定的运动员,甲、乙两名运动员平时训练成绩的方差分别为S甲2=0.03,S乙2=0.20,你认为教练应该挑选的运动员是( )
A.乙
B.甲
C.甲、乙都行
D.无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com