
 如图所示,某工厂的大门是抛物线形水泥建筑物,大门的地面宽度为8m,两侧距地面3m高处各有一壁灯,两壁灯间的水平距离为6m,则厂门的高度约为6.9m.(精确到0.1m)
如图所示,某工厂的大门是抛物线形水泥建筑物,大门的地面宽度为8m,两侧距地面3m高处各有一壁灯,两壁灯间的水平距离为6m,则厂门的高度约为6.9m.(精确到0.1m) 分析 由题意可知,以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,抛物线过A(0,0)、B(8,0)、(1、3)、(7、3),运用待定系数法求出解析式后,求函数值的最大值即可.
解答 解:以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,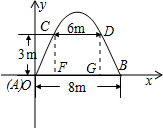
则抛物线过A(0,0)、B(8,0)、C(1、3)、D(7、3)四点,
设该抛物线解析式为:y=ax2+bx+c,
则$\left\{\begin{array}{l}{c=0}\\{64a+8b+c=0}\\{a+b+c=3}\end{array}\right.$,
解得:
$\left\{\begin{array}{l}{a=-\frac{3}{7}}\\{b=\frac{24}{7}}\end{array}\right.$.
函数解析式为:y=-$\frac{3}{7}$x2+$\frac{24}{7}$x.
当x=4时,可得y=-$\frac{48}{7}$+$\frac{96}{7}$=$\frac{48}{7}$≈6.9米.
故答案为:6.9 m.
点评 本题考查点的坐标的求法及二次函数的实际应用,关键是建立数学模型,借助二次函数解决实际问题,注意根据线段长度得出各点的坐标.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
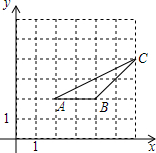 如图,△ABC的三个顶点坐标分别为A(2,2)、B(4,2)、C(6,4),以原点O为位似中心,将△ABC缩小,使变换后得到的A′B′C′与△ABC对应边的比为1:2,画出A′B′C′,直接求出点A′、B′、C′的坐标.
如图,△ABC的三个顶点坐标分别为A(2,2)、B(4,2)、C(6,4),以原点O为位似中心,将△ABC缩小,使变换后得到的A′B′C′与△ABC对应边的比为1:2,画出A′B′C′,直接求出点A′、B′、C′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )| A. | $\widehat{AC}$ | B. | $\widehat{AD}$ | C. | $\widehat{ACD}$ | D. | $\widehat{ADB}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com