
”¾ĢāÄæ”æijŠ£ĪŖĆĄ»ÆŠ£Ō°£¬°²Åżה¢ŅŅĮ½øö¹¤³Ģ¶Ó½ųŠŠĀĢ»Æ£®ŅŃÖŖ¼×¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿ŹĒŅŅ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆĆ껿µÄ2±¶£¬²¢ĒŅŌŚø÷×Ō¶ĄĮ¢Ķź³ÉĆ껿ĪŖ400m2ĒųÓņµÄĀĢ»ÆŹ±£¬¼×¶Ó±ČŅŅ¶ÓÉŁÓĆ4Ģģ£®
£Ø1£©Ēó¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿·Ö±šŹĒ¶ąÉŁm2£æ
£Ø2£©ČōĀĢ»ÆĒųÓņĆ껿ĪŖ1800m2£¬Ń§Š£ĆæĢģŠčø¶øų¼×¶ÓµÄĀĢ»Æ·ŃÓĆĪŖ0.4ĶņŌŖ£¬ĆæĢģŠčø¶øųŅŅ¶ÓµÄĀĢ»Æ·ŃÓĆĪŖ0.25ĶņŌŖ£¬Éč°²Åż׶ӹ¤×÷yĢģ£¬ĀĢ»Æ×Ü·ŃÓĆĪŖWĶņŌŖ£®
¢ŁĒóWÓėyµÄŗÆŹż¹ŲĻµŹ½£»
¢ŚŅŖŹ¹Õā“ĪµÄĀĢ»Æ×Ü·ŃÓĆ²»³¬¹ż8ĶņŌŖ£¬ÖĮÉŁÓ¦°²Åż׶ӹ¤×÷¶ąÉŁĢģ£æ
”¾“š°ø”æ£Ø1£©¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿·Ö±šŹĒ100m2”¢50m2£»£Ø2£©¢ŁŗÆŹż±ķ“ļŹ½ĪŖw=©0.1y+9£¬¢ŚÖĮÉŁÓ¦°²Åż׶ӹ¤×÷10Ģģ.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÉčŅŅ¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿ŹĒx£Øm2£©£¬øł¾ŻŌŚ¶ĄĮ¢Ķź³ÉĆ껿ĪŖ400m2ĒųÓņµÄĀĢ»ÆŹ±£¬¼×¶Ó±ČŅŅ¶ÓÉŁÓĆ4Ģģ£¬ĮŠ³ö·½³Ģ£¬Ēó½ā¼“æÉ£»
£Ø2£©¢ŁÓĆŗ¬yµÄ“śŹżŹ½±ķŹ¾³öŅŅĶź³É¹¤×÷ĖłŠčŅŖµÄĢģŹż£¬øł¾Ż×Ü·ŃÓĆ=¼×µÄ·ŃÓĆ+ŅŅµÄ·ŃÓĆ£¬¼“æÉµĆ³öŗÆŹż¹ŲĻµŹ½£»
¢Śøł¾Ż×Ü·ŃÓĆ²»³¬¹ż8ĶņŌŖ£¬ĮŠ²»µČŹ½½ųŠŠĒó½ā¼“æɵĆ.
ŹŌĢā½āĪö£ŗ£Ø1£©ÉčŅŅ¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿ŹĒx£Øm2£©£¬øł¾ŻĢāŅāµĆ
![]() £¬
£¬
½āµĆ£ŗx=50£¬
¾¼ģŃé£ŗx=50ŹĒŌ·½³ĢµÄ½ā£¬
ĖłŅŌ¼×¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿ŹĒ50”Į2=100£Øm2£©£¬
“š£ŗ¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿·Ö±šŹĒ100m2”¢50m2£»
£Ø2£©¢Ł¼×¶Ó¹¤×÷yĢģĶź³É£ŗ100y£Øm2£©£¬ŅŅ¶ÓĶź³É¹¤×÷ĖłŠčŅŖ£ŗ ![]() £ØĢģ£©£¬
£ØĢģ£©£¬
”ąw=0.4y+0.25”Į![]() =0.1y+9£»
=0.1y+9£»
¢Śµ±×Ü·ŃÓĆw²»³¬¹ż8ĶņŌŖŹ±£¬9©0.1y”Ü8£¬
½āµĆy”Ż10£¬
“š£ŗÖĮÉŁÓ¦°²Åż׶ӹ¤×÷10Ģģ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒÓĆĘå×Ó°Ś³ÉµÄ”°ÉĻ”±×Ö£®

(1)ŅĄÕÕ“Ė¹ęĀÉ£¬µŚ4øöĶ¼ŠĪŠčŅŖŗŚ×Ó”¢°××Óø÷¶ąÉŁĆ¶£æ
(2)°“ÕÕÕāŃłµÄ¹ęĀÉ°ŚĻĀČ„£¬°Ś³ÉµŚnøö”°ÉĻ”±×ÖŠčŅŖŗŚ×Ó”¢°××Óø÷¶ąÉŁĆ¶£æ
(3)ĒėĢ½¾æµŚ¼øøö”°ÉĻ”±×ÖĶ¼ŠĪ°××Ó×ÜŹż±ČŗŚ×Ó×ÜŹż¶ą15ƶ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµćA£¬O£¬BŹĒŹżÖįÉĻ“Ó×óÖĮÓŅµÄČżøöµć£¬ĘäÖŠOÓėŌµćÖŲŗĻ£¬µćA±ķŹ¾µÄŹżĪŖ©4£¬ĒŅAO+AB£½11£®
![]()
£Ø1£©Ēó³öµćBĖł±ķŹ¾µÄŹż£¬²¢ŌŚŹżÖįÉĻ°ŃµćB±ķŹ¾³öĄ“£®
£Ø2£©µćCŹĒŹżÖįÉĻµÄŅ»øöµć£¬ĒŅCA£ŗCB£½1£ŗ2£¬ĒóµćC±ķŹ¾µÄŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£°ĖÄź¼¶(1)°ąČ«Ģåѧɜ½ųŠŠĮĖµŚŅ»“ĪĢåÓżÖŠæ¼Ä£Äā²āŹŌ£¬³É¼ØĶ³¼ĘČēĻĀ±ķ£ŗ
³É¼Ø(·Ö) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
ČĖŹż(ČĖ) | 6 | 5 | 5 | 8 | 7 | 7 | 4 |
øł¾ŻÉĻ±ķÖŠµÄŠÅĻ¢ÅŠ¶Ļ£¬ĻĀĮŠ½įĀŪÖŠ“ķĪóµÄŹĒ( )
A. øĆ°ąŅ»¹²ÓŠ42ĆūĶ¬Ń§
B. øĆ°ąŃ§ÉśÕā“Īæ¼ŹŌ³É¼ØµÄÖŚŹżŹĒ8
C. øĆ°ąŃ§ÉśÕā“Īæ¼ŹŌ³É¼ØµÄĘ½¾łŹżŹĒ27
D. øĆ°ąŃ§ÉśÕā“Īæ¼ŹŌ³É¼ØµÄÖŠĪ»ŹżŹĒ27·Ö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶Ōx£¬y¶ØŅåŅ»ÖÖŠĀŌĖĖćT£¬¹ę¶Ø£ŗT£Øx£¬y£©=![]() £ØĘäÖŠa”¢b¾łĪŖ·ĒĮć³£Źż£©£¬ÕāĄļµČŹ½ÓŅ±ßŹĒĶس£µÄĖÄŌņŌĖĖć£¬ĄżČē£ŗT£Ø0£¬1£©=
£ØĘäÖŠa”¢b¾łĪŖ·ĒĮć³£Źż£©£¬ÕāĄļµČŹ½ÓŅ±ßŹĒĶس£µÄĖÄŌņŌĖĖć£¬ĄżČē£ŗT£Ø0£¬1£©=![]() =b£®
=b£®
£Ø1£©ŅŃÖŖT£Ø1£¬©1£©=©2£¬T£Ø4£¬2£©=1£®
¢ŁĒóa£¬bµÄÖµ£»
¢ŚČō¹ŲÓŚmµÄ²»µČŹ½×é![]() Ē”ŗĆÓŠ3øöÕūŹż½ā£¬Ē󏵏żpµÄȔֵ·¶Ī§£»
Ē”ŗĆÓŠ3øöÕūŹż½ā£¬Ē󏵏żpµÄȔֵ·¶Ī§£»
£Ø2£©ČōT£Øx£¬y£©=T£Øy£¬x£©¶ŌČĪŅāŹµŹżx£¬y¶¼³ÉĮ¢£ØÕāĄļT£Øx£¬y£©ŗĶT£Øy£¬x£©¾łÓŠŅāŅ壩£¬Ōņa£¬bÓ¦Āś×ćŌõŃłµÄ¹ŲĻµŹ½£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚĢŻŠĪABCDÖŠ£¬AB”ĪCD£¬”ĻD=90”ć£¬AD=CD=2£¬µćEŌŚ±ßADÉĻ£Ø²»ÓėµćA”¢DÖŲŗĻ£©£¬”ĻCEB=45”ć£¬EBÓė¶Ō½ĒĻßACĻą½»ÓŚµćF£¬ÉčDE=x£®
£Ø1£©ÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾Ļ߶ĪCFµÄ³¤£»
£Ø2£©Čē¹ū°Ń”÷CAEµÄÖܳ¤¼Ē×÷C”÷CAE£¬”÷BAFµÄÖܳ¤¼Ē×÷C”÷BAF£¬Éč![]() =y£¬Ēóy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öĖüµÄ¶ØŅåÓņ£»
=y£¬Ēóy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öĖüµÄ¶ØŅåÓņ£»
£Ø3£©µ±”ĻABEµÄÕżĒŠÖµŹĒ![]() Ź±£¬ĒóABµÄ³¤£®
Ź±£¬ĒóABµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
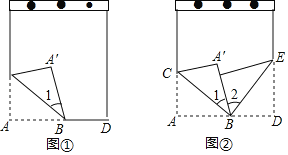
”¾ĢāÄæ”æČēĶ¼¢Ł£¬½«±Ź¼Ē±¾»īŅ³Ņ»½ĒÕŪ¹żČ„£¬Ź¹½ĒµÄ¶„µćAĀäŌŚA”䓦£¬BCĪŖÕŪŗŪ£»
£Ø1£©Ķ¼¢ŁÖŠ£¬Čō”Ļ1£½30”ć£¬Ōņ”ĻA”äBD£½_____£»
£Ø2£©Čē¹ūŌŚĶ¼¢ŚÖŠøıä”Ļ1µÄ“󊔣¬ŌņBAµÄĪ»ÖĆŅ²ĖęÖ®øı䣬ÓÖ½«»īŅ³µÄĮķŅ»½ĒŠ±ÕŪ¹żČ„£¬Ź¹BD±ßÓėBA”äÖŲŗĻ£¬ÕŪŗŪĪŖBE£®ÄĒĆ“”ĻCBEµÄ¶ČŹżŹĒ·ń»į·¢Éś±ä»ÆÄŲ£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć£ŗ
£Ø1£©©4.2+5.7©5.8+10
£Ø2£©£Ø©3£©”Į£Ø©4£©©60”Ā|©12|
£Ø3£©![]()
£Ø4£©©14+[£Ø©3£©2©£Ø1©22£©”Į2]
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚ”÷ABCÓė”÷ADEÖŠ£¬AB=AC£¬AD=AE£¬”ĻAŹĒ¹«¹²½Ē”£
£Ø1£©BDÓėCEµÄŹżĮæ¹ŲĻµŹĒ£ŗBD______CE£»
£Ø2£©°ŃĶ¼¢Ł”÷ABCČʵćAŠż×ŖŅ»¶ØµÄ½Ē¶Č£¬µĆµ½ČēĶ¼¢ŚĖłŹ¾µÄĶ¼ŠĪ”£
¢ŁĒóÖ¤£ŗBD£½CE£»
¢ŚBDÓėCEĖłŌŚÖ±ĻߵļŠ½ĒÓė”ĻDAEµÄŹżĮæ¹ŲĻµŹĒŹ²Ć“£æĖµĆ÷ĄķÓÉ”£
£Ø3£©ČōAD=10£¬AB=6£¬°ŃĶ¼¢ŁÖŠµÄ”÷ABCČʵćAĖ³Ź±ÕėŠż×Ŗ¦Į¶Č(0”ć<¦Į”Ü360)Ö±½ÓŠ“³öBD³¤¶ČµÄȔֵ·¶Ī§”£

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com