练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，正方形ABCD中，E，F分别是BC，CD边上的点，AE，DE，BF，AF把正方形分成8小块，试比较S3与S2+S7+S8的大小，并说明理由．

    分析 根据图示可知，S3=SABCD-S△ABE-S△BCF-S△CDE-S△ADF+S2+S7+S8，根据本等量关系式求解．

    解答 解：S3=S2+S7+S8．
    理由：如图，图中S3的面积
    S3=SABCD-S△ABE-S△BCF-S△CDE-S△ADF+S2+S7+S8
    化简得S3=BC•CD-$\frac{1}{2}$×（BE+EC）×CD-$\frac{1}{2}$×（DF+FC）×BC+S2+S7+S8
    ∵BC=CD，
    ∴BC•CD=$\frac{1}{2}$×（BE+EC）×CD+$\frac{1}{2}$×（DF+FC），
    故S3=S2+S7+S8．

    点评 本题考查了正方形邻边互相垂直，且四边相等的性质，用转换思想，把S3用正方形面积减去其他图形的面积求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．观察日历可以发现横排相邻的两个日期数大小相差1，上、下相邻的两个日期数相差7；若横排相邻的两个日期数之和为15，设较小的一个日期数为x，则可列方程x+x+1=15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知（x-1）2+|y+2|=0，求（5xy-2x2）-2（3xy-4x2）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

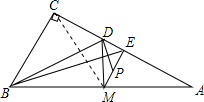    14．如图，Rt△ABC中，∠C=90°，点D在AC上，BD=AD，M是AB的中点，AE⊥AC于E，点P是ME的中点，连接DP，求证：BE⊥DP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知任意四边形ABCD，边AD、BC的中点分别为E、F，求证：$\overrightarrow{EF}$=$\frac{1}{2}$（$\overrightarrow{AB}$$+\overrightarrow{DC}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图所示，在四边形ABCD中．AB=AD，∠BAD=∠C=90°，BC=5，CD=3，过点A作AE⊥BC，垂足为点E，请你利用旋转变换求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，若OA：OD=OB：OC=n，则x=$\frac{a-bn}{2}$．（用a，b，n表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，四边形ABCD和四边形A′B′C′D′是位似图形．若OA：AA′=1：2，求四边形ABCD与四边形A′B′C′D′的面积之比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，点E是?ABCD中BC边延长线上一点，AE交CD于F，则图中的相似三角形有3对．

    查看答案和解析>>

    同步练习册答案