
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(![]() )求证:
)求证:![]() .
.
(![]() )若
)若![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.

【答案】(![]() )见解析(
)见解析(![]() )
)![]()
【解析】试题分析:
(1)由已知条件易证∠GAD=∠ADE=∠CED,结合∠AGE=∠GAD+∠ADE,可得∠AGE=2∠CED,再结合∠AED=2∠CED即可得到∠AGE=∠AED,从而可得AE=AG;
(2)如下图,连接GH,由(1)中结论可知AE=AG=![]() ,结合BE=2,在Rt△ABE中可求得AB=11,结合BF=1可求得AF=10,再结合G是DF的中点,H是AD的中点由三角形中位线定理即可求得GH=5.
,结合BE=2,在Rt△ABE中可求得AB=11,结合BF=1可求得AF=10,再结合G是DF的中点,H是AD的中点由三角形中位线定理即可求得GH=5.
试题解析:
(![]() )∵ 四边形
)∵ 四边形![]() 是矩形,
是矩形,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,
又∵ ![]() 为
为![]() 中点,
中点,
∴ ![]() ,
,
∴ ![]() ,
,
∵∠AGE=∠GAD+∠ADE,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]() ,
,
![]() .
.
(![]() )连接
)连接![]() ,由(
,由(![]() )知:
)知:![]() =
=![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∵ ![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,
∴ ![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=![]() ∠B=
∠B=![]() ∠C;
∠C;
④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有( )
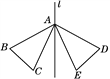
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设购买甲种树苗x棵,有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x的式子表示);
树苗类型 | 甲种树苗 | 乙种树苗 |
购买树苗数量(单位:棵) | x | |
购买树苗的总费用(单位:元) |
②如果购买甲、乙两种树苗共用去25 600元,那么甲、乙两种树苗各购买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26 000元,求n的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a![]() b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2
b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2![]() 5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2) ![]() 3的值;
3的值;
(2)若3![]() x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:问 题:如图1,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为6,8,10,求∠APB的度数?


分 析:由于PA,PB,PC不在同一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′和△ABP全等,这样,就可以利用全等三角形知识,将三条线段的长度转化到同一个三角形中从而求出∠APB的度数.
(1)请你按上述方法求出图1中∠APB的度数;
(2)请你利用第(1)题的解答思想方法,解答下面问题:如图2,已知△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°,求证:EF2=BE2+FC2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com