
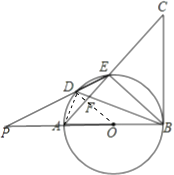
【题目】如图,AB是⊙O的直径,点D是 ![]() 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F. 
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DFDB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径.
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∵∠EDB=∠EAB,∠BDE=∠CBE,
∴∠EAB=∠CBE,
∴∠ABE+∠CBE=90°,
∴CB⊥AB,
∵AB是⊙O的直径,
∴BC是⊙O的切线;
(2)证明:∵BD平分∠ABE,
∴∠ABD=∠DBE, ![]() =
= ![]() ,
,
∴∠DEA=∠DBE,
∵∠EDB=∠BDE,
∴△DEF∽△DBE,
∴ ![]() =
= ![]() ,
,
∴DE2=DFDB;
(3)解:连接DA、DO,
∵OD=OB,
∴∠ODB=∠OBD,
∵∠EBD=∠OBD,
∴∠EBD=∠ODB,
∴OD∥BE,
∴ ![]() =
= ![]() ,
,
∵PA=AO,
∴PA=AO=OB,
∴ ![]() =
= ![]()
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵DE=2,
∴PD=4,
∵∠PDA+∠ADE=180°,∠ABE+∠ADE=180°,
∴∠PDA=∠ABE,
∵OD∥BE,
∴∠AOD=∠ABE,
∴∠PDA=∠AOD,
∵∠P=∠P,
∴△PDA∽△POD,
∴ ![]() =
= ![]() ,
,
设OA=x,
∴PA=x,PO=2x,
∴ ![]() =
= ![]() ,
,
∴2x2=16,x=2 ![]() ,
,
∴OA=2 ![]() .
.
【解析】(1)根据圆周角定理即可得出∠EAB+∠EBA=90°,再由已知得出∠ABE+∠CBE=90°,则CB⊥AB,从而证得BC是⊙O的切线;(2)通过证得△DEF∽△DBE,得出相似三角形的对应边成比例即可证得结论.(3)连接DA、DO,先证得OD∥BE,得出 ![]() =
= ![]() ,然后根据已知条件得出
,然后根据已知条件得出 ![]() =
= ![]() =
= ![]() =
= ![]() ,求得PD=4,通过证得△PDA∽△POD,得出
,求得PD=4,通过证得△PDA∽△POD,得出 ![]() =
= ![]() ,设OA=x,则PA=x,PO=2x,得出
,设OA=x,则PA=x,PO=2x,得出 ![]() =
= ![]() ,解得OA=2
,解得OA=2 ![]() .
.
【考点精析】根据题目的已知条件,利用切线的判定定理和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】按要求完成下列证明:
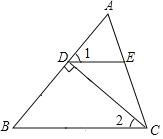
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知),
∴∠1+ =90°( ).
∵∠1+∠2=90°(已知),
∴ =∠2( ).
∴DE∥BC( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实数范围内定义一种运算“*”,其运算法则为a*b=a2﹣ab.根据这个法则,下列结论中正确的是_______.(把所有正确结论的序号都填在横线上)
①![]() *
*![]() =2﹣
=2﹣![]() ;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=
;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=![]() ,x2=
,x2=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
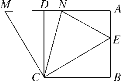
【题目】如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CE,CM.
(1)求证:∠BCE=∠DCM;
(2)若点N在边AD上,且∠NCE=45°,连接NC,NE,求证:NE=BE+DN;
(3)在(2)的条件下,若DN=2,MD=3,求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米. 
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1 , 第二次将点A1向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 则A3表示的数是按照这种移动规律移动下去,第n次移动到点AN , 如果点AN与原点的距离不小于20,那么n的最小值是 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,![]() OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将
OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将![]() OABC的面积平分,则b=_______.
OABC的面积平分,则b=_______.
(2)在平面直角坐标系中,直线y=2x+3关于原点对称的直线的表达式为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
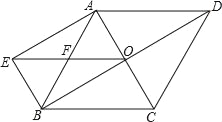
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com