
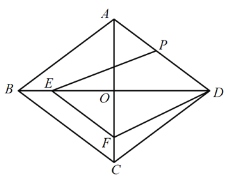
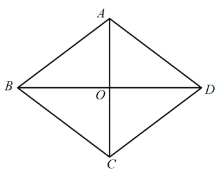
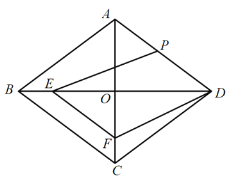
【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,且AC=12cm,BD=16cm,点P从点D出发,沿DA方向匀速向点A运动,速度为2cm/s;同时,点E从点B出发,沿BO方向匀速向点O运动,速度为1cm/s,EF∥BC,交OC于点F.当点P、E中有一点停止运动时,另一点也停止运动,线段EF也停止运动,连接PE、DF(0<t<5).解答下列问题:
(1)当t为何值时,PE∥AB?
(2)设四边形EFDP的面积为y(![]() ),求y与t之间的函数关系式.
),求y与t之间的函数关系式.
(3)是否存在某一时刻t,使得![]() ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.
(4)连接FP,是否存在某一时刻t,使得FP⊥AD?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)t=![]() s;(2)
s;(2)![]() ;(3)不存在,理由见解析;(4)存在, t=
;(3)不存在,理由见解析;(4)存在, t=![]()
【解析】
(1)由菱形性质和勾股定理求得菱形的边长![]() ,然后利用平行线分线段成比例定理得到
,然后利用平行线分线段成比例定理得到![]() ,然后将BE=t,DE=16-t,DP=2t代入求解即可;
,然后将BE=t,DE=16-t,DP=2t代入求解即可;
(2)作PQ⊥OD于Q,利用AA定理判定△DQP∽△DOA,然后根据相似三角形性质求得PQ的长,利用平行线分线段成比例定理求得OF的长,从而利用三角形面积公式求函数解析式;
(3)由(2)问中求得的四边形面积与菱形面积的等量关系![]() 列方程求解;
列方程求解;
(4)假设存在t,使得FP⊥AD,由AA定理证得△AOD∽△APF,然后根据相似三角形的性质求得![]() ,从而列方程求解即可.
,从而列方程求解即可.
解:(1)由题意可知:BE=t,DE=16-t,DP=2t
∵四边形ABCD是菱形,
∴![]() ,
,
![]() ,
,
AC⊥BD,AB=BC=CD=DA,
∴在Rt△AOD中,
由勾股定理,得
![]() ,
,
∴![]() ,
,
∵PE∥AB,
∴![]() ,
,
即,![]() ,
,
∴![]() ,
,
因此,当t为![]() s时,PE∥AB.
s时,PE∥AB.
(2)作PQ⊥OD于Q,
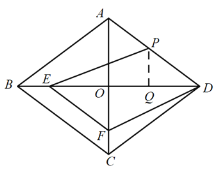
∴∠DQP=∠DOA=90°,
又∵∠QDP=∠ODA,
∴△DQP∽△DOA,
∴![]() ,
,
即,![]() ,
,
∴![]() ,
,
∵EF∥BC,
∴![]() ,
,
即,![]() ,
,
∴![]() ,
,
∴![]()
![]()
因此,y与t之间的函数关系式为![]() .
.
(3)假设存在t,使得![]() ,
,
∴![]() ,
,
即,![]() ,
,
∴![]() ,
,
解得,![]() ,
,![]() ,均不符合题意,
,均不符合题意,
因此,不存在t,使![]() .
.
(4)假设存在t,使得FP⊥AD.
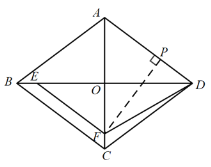
∵四边形ABCD是菱形
∴AC⊥BD=90°,
∴∠AOD=90°,
∵FP⊥AD
∴∠APF=90°,
∴∠AOD=∠APF,
∵∠OAD=∠PAF,
∴△AOD∽△APF
∴![]()
∵![]() ,DP=2t
,DP=2t
∴AF=![]() ,AP=10-2t
,AP=10-2t
∴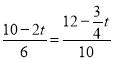
∴t=![]()
因此,当t=![]() 时,FP⊥AD.
时,FP⊥AD.


科目:初中数学 来源: 题型:
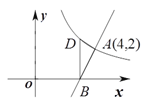
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]()
![]() 轴交反比例函数的图象于点
轴交反比例函数的图象于点![]() ,求点D的坐标和
,求点D的坐标和![]() 的面积;
的面积;
(3)观察图象,写出当x>0时不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y![]() x的图象与性质.
x的图象与性质.
小亮根据学习函数的经验,对函数y![]() x的图象与性质进行了探究.
x的图象与性质进行了探究.
下面是小亮的探究过程,请补充完整:
(1)函数y![]() x中自变量x的取值范围是 ;
x中自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 |
|
|
|
| 3 | 4 | 5 | 6 | … |
y | … |
|
|
| 0 |
|
|
|
| m |
|
|
| … |
求m的值;
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
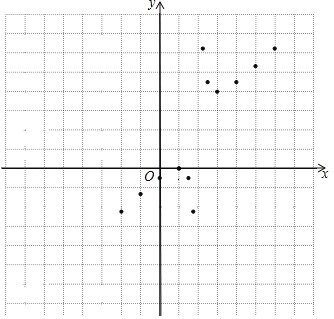
(4)根据画出的函数图象,发现下列特征:
①该函数的图象是中心对称图形,对称中心的坐标是 ;
②该函数的图象与过点(2,0)且平行于y轴的直线越来越靠近而永不相交,该函数的图象还与直线 越来越靠近而永不相交.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告.已知当这种商品每月的广告费用为m(千元)时,每月销售量将是原销售量的p倍,且p =![]() .
.
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽学生视野,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级开展研学旅行活动,在参加此次活动的师生中,若每位老师带![]() 名学生,还剩
名学生,还剩![]() 名学生没人带;若每位老师带
名学生没人带;若每位老师带![]() 名学生,则有一位老师少带
名学生,则有一位老师少带![]() 名学生.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
名学生.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 已和客车 | |
载客量(人/量) |
|
|
租金(元/辆) |
|
|
学校计划此次研学旅行活动的租车总费用不超过![]() 元,为了安全,每辆客车上至少要有
元,为了安全,每辆客车上至少要有![]() 名老师.
名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有![]() 名老师,可求得租用客车总数为______辆.
名老师,可求得租用客车总数为______辆.
(3)在(2)的条件下,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“停课不停学,学习不延期”,某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”,为了解学生每天的学习时间情况,在全市随机抽取了部分初中学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
组别 | 学习时间x(h) | 人数(人) |
A | 2.5<x≤3 | 40 |
B | 3<x≤3.5 | 170 |
C | 3.5<x≤4 | 350 |
D | 4<x≤4.5 | |
E | 4.5<x≤5 | 90 |
F | 5小时以上 | 50 |
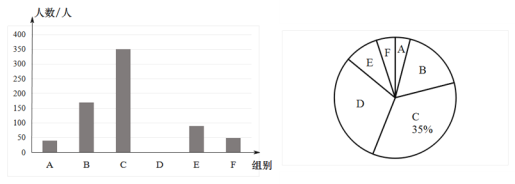
(1)这次参与问卷调查的初中学生有 人,中位数落在 组.
(2)补全条形统计图.
(3)若此市有初中学生2.8万人,求每天参与“空中课堂”学习时间3.5到4.5小时(不包括3.5小时)的初中学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG= 2BE.设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
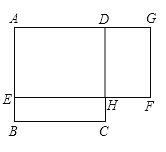
(1)求y与x之间的函数关系式(不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,顶点O(0,0),A(﹣2,3),B(2,3),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第2020次旋转结束时,点D的坐标为( )
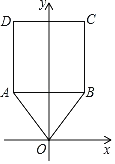
A.(﹣2,7)B.(7,2)C.(2,﹣7)D.(﹣7,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() )的图象经过点
)的图象经过点![]() 和
和![]() ,直线
,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
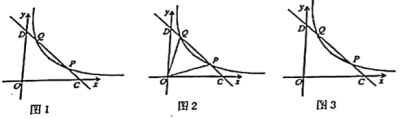
(1)求![]() 的度数;
的度数;
(2)如图2,连接![]() 、
、![]() ,当
,当![]() 时,求此时
时,求此时![]() 的值:
的值:
(3)如图3,点![]() ,点
,点![]() 分别在
分别在![]() 轴和
轴和![]() 轴正半轴上的动点.再以
轴正半轴上的动点.再以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .若点
.若点![]() 恰好在函数
恰好在函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() )的图象上,且四边形
)的图象上,且四边形![]() 为平行四边形,求此时
为平行四边形,求此时![]() 、
、![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com