
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
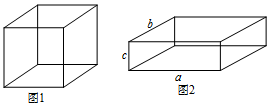
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
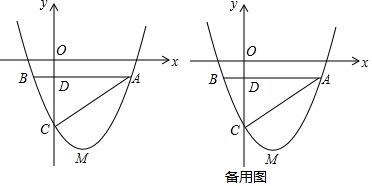
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
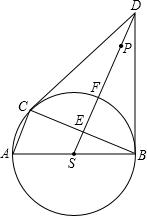 如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.
如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 判别式△=b2-4ac | △>0 | △=0 | △<0 |
| 二次函数y=ax2+bx+c(a>0)的图象 | 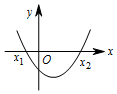 |  | 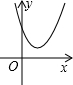 |
| 一元二次方程y=ax2+bx+c(a>0)的根 | 有两个不相等的实数根 x1=$\frac{-b+\sqrt{△}}{2a}$,x2=$\frac{-b-\sqrt{△}}{2a}$(x1<x2) | 有两个相等的实数根 x1=x2=-$\frac{b}{2a}$ | 无实数根 |
| 使y>0的x的取值范围 | x<x1或x>x2 | x≠-$\frac{b}{2a}$ | 全体实数 |
| 不等式ax2+bx+c>0(a>0)的解集 | 无解 | x≠-$\frac{b}{2a}$ | 无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com