
【题目】某商场试销一种成本价为每件60元的服装,规定试销期间销售单价不低于成本单价,获利不得高于40%.经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=80时,y=40;x=70时,y=50.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
【答案】(1)一次函数的解析式为y=﹣x+120(60≤x≤84);(2)销售价定为每件84元时,可获得最大利润,最大利润是864元.
【解析】试题分析:(1)根据题意得:销售单价x≥成本60元,获利不得高于40%,则销售单价x≤60(1+40%);再利用待定系数法把x=80时,y=40;x=70时,y=50代入一次函数y=kx+b中,求出k,b即可得到关系式;
(2)根据题目意思,表示出销售额和成本,然后表示出利润=销售额-成本,整理后根据x的取值范围求出最大利润.
试题解析:(1)60≤x≤60(1+40%),
∴60≤x≤84,
由题得:![]() ,解得:k=﹣1,b=120,
,解得:k=﹣1,b=120,
∴一次函数的解析式为y=﹣x+120(60≤x≤84);
(2)销售额:xy=x(﹣x+120)元;成本:60y=60(﹣x+120),
∴W=xy﹣60y,
=x(﹣x+120)﹣60(﹣x+120),
=(x﹣60)(﹣x+120),
=﹣x2+180x﹣7200,
=﹣(x﹣90)2+900,
∴W=﹣(x﹣90)2+900,(60≤x≤84),
当x=84时,W取得最大值,最大值是:﹣(84﹣90)2+900=864(元),
即销售价定为每件84元时,可获得最大利润,最大利润是864元.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
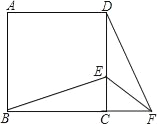
【题目】如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠BEC=60°,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且﹣1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( )

A. y1<y2<y3 B. y3<y1<y2 C. y3<y2<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:善于思考的小明在解方程组![]() 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:![]() 请你解决以下问题:
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组![]()
(2)已知 x、y、z,满足![]() 试求 z 的值.
试求 z 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据图中信息解答下列问题:
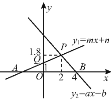
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
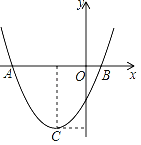
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(﹣1,﹣3),与x轴交于A(﹣3,0)、B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在图(1)与图(2)中,每个小方格都是边长为1个单位的正方形,![]() 的三个顶点都在格点上.
的三个顶点都在格点上.
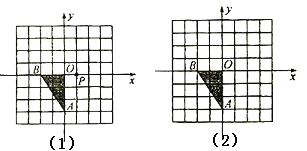
(1)将![]() 关于点
关于点![]() 对称,在图(1)中画出对称后的图形
对称,在图(1)中画出对称后的图形![]() ,并涂黑;
,并涂黑;
(2)将△OAB先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,腰AB的垂直平分线DE交AB于点E,交AC于点D,且∠DBC=15°,则∠A的度数是 ( )

A.50°B.36°C.40°D.45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com