
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 在
在![]() 上以每秒
上以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动.点
运动.点![]() 沿
沿![]() 方向以每秒1个单位长度的速度运动,当点
方向以每秒1个单位长度的速度运动,当点![]() 不与点
不与点![]() 重合时,连结
重合时,连结![]() ,以
,以![]() ,
,![]() 为邻边作
为邻边作![]() .当点
.当点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动,设点
也随之停止运动,设点![]() 的运动时间为
的运动时间为![]() ,
,![]() 与
与![]() 重叠部分的图形面积为
重叠部分的图形面积为![]() .
.
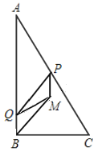
(1)点![]() 到边
到边![]() 的距离
的距离![]() ,点
,点![]() 到边
到边![]() 的距离
的距离![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落在线段
落在线段![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)连结![]() ,当
,当![]() 与
与![]() 的一边平行或垂直时,直接写出
的一边平行或垂直时,直接写出![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3) ;(4)
;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)过![]() 作
作![]() ,勾股定理求出AC,表达出
,勾股定理求出AC,表达出![]() ,
,![]() ,利用锐角三角函数求出PE,AE即可解答;
,利用锐角三角函数求出PE,AE即可解答;
(2)当点![]() 落在线段
落在线段![]() 上时,证明四边形PMBQ是矩形,从而得到
上时,证明四边形PMBQ是矩形,从而得到![]() ,解出t的值即可;
,解出t的值即可;
(3)分两种情况讨论,①当![]() 时,
时,![]() 与
与![]() 重叠面积为
重叠面积为![]() ,根据已有数据即可计算得出;②当
,根据已有数据即可计算得出;②当![]() 时,则
时,则![]() 与
与![]() 重叠面积为
重叠面积为![]() ,根据已有数据计算即可;
,根据已有数据计算即可;
(4)①如图,当![]() 时,证明四边形EPMQ是矩形,得到
时,证明四边形EPMQ是矩形,得到![]() 解出t即可;②当
解出t即可;②当![]() 时,延长
时,延长![]() 交
交![]() 于X,通过
于X,通过![]() ,利用锐角三角函数得出
,利用锐角三角函数得出![]() ,以及AQ的值,列出方程
,以及AQ的值,列出方程![]() 即可解出t的值;③当
即可解出t的值;③当![]() ,证明四边形
,证明四边形![]() 是平行四边形,列出方程
是平行四边形,列出方程![]() ,即可解出t的值.
,即可解出t的值.
(1)过![]() 作
作![]() ,由题意可知
,由题意可知![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴AC=![]() ,
,
∴![]() ,
,![]() ,
,
∴PE=![]() ,AE=
,AE=![]() ,
,
则![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() .
.
故答案为:![]() ;
;![]() ;
;
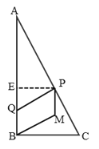
(2)当点![]() 落在线段
落在线段![]() 上时,
上时,
∵四边形PMBQ是平行四边形,
∴PM∥BQ,PM⊥BC,
∴四边形PMBQ是矩形,
∴![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
解得:![]()

(3)①当![]() 时
时
![]() 与
与![]() 重叠面积为
重叠面积为![]()
![]()
由(1)可知![]() ,
,![]()
![]()
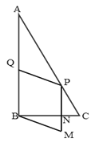
②当![]() 时,设PM交BC于点N,
时,设PM交BC于点N,
则![]() 与
与![]() 重叠面积为
重叠面积为![]()
![]()
∵由(1)可知,![]() ,
,![]() ,
,![]()
![]()
![]() .
.
综上所述, ;
;
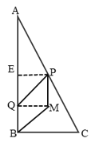
(4)①如图,当![]() 时,则
时,则![]() .
.
由(1)得:![]() ,
,![]() .
.
∵PM∥EQ,EP∥MQ,且QM⊥AB,
∴四边形EPMQ是矩形,
∴![]()
![]() ,解得:
,解得:![]() .
.
②当![]() 时,延长
时,延长![]() 交
交![]() 于X
于X
![]() ,
,![]() .
.
![]() ,
,
又![]()
![]()
![]() .
.
又![]()
![]()
解得:![]() .
.
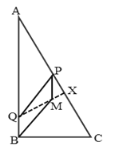
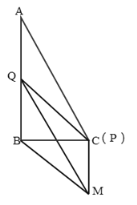
③当![]()
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]() .
.
![]()
![]() .
.
综上所述,当![]() 与
与![]() 的一边平行或垂直时,
的一边平行或垂直时,![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x(单位:min) | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y(单位:℃) | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为 ;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式 ;
当4<x≤16时,写出一个符合表中数据的函数解析式 ;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源 min.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的边
的边![]() 的垂直平分线,垂足为点
的垂直平分线,垂足为点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则下列结论:
,则下列结论:
①四边形![]() 是菱形;
是菱形;
②![]() ;
;
③![]() ;
;
④![]() 四边形
四边形![]()
以上四个结论中所有正确的结论是( )

A.①②B.①②③C.②④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
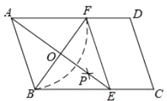
【题目】如图所示,在![]() 中,以
中,以![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 于点
于点![]() ,再分别以点
,再分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 为半径画弧,两弧交于一点
为半径画弧,两弧交于一点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .若
.若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为____.
的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、
丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
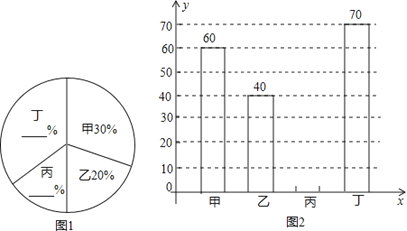
(1)这四个班共植树 棵;
(2)请你在答题卡上补全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
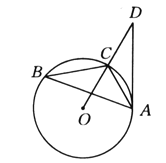
【题目】如图所示,已知△ABC内接于⊙O,点D在OC的延长线上,sin B=![]() ,∠D=30°.
,∠D=30°.
(1)求证AD是⊙O的切线;
(2)若AC=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
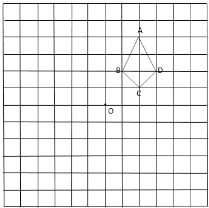
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知格点四边形![]() (顶点是网格线的交点)和格点
(顶点是网格线的交点)和格点![]() .
.
(1)将四边形![]() 先向左平移4个单位长度,再向下平移6个单位长度,得到四边形
先向左平移4个单位长度,再向下平移6个单位长度,得到四边形![]() ,画出平移后的四边形
,画出平移后的四边形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)将四边形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到四边形
,得到四边形![]() ,画出旋转后的四边形
,画出旋转后的四边形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() ,
,![]() );
);
(3)填空:点![]() 到
到![]() 的距离为________.
的距离为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,AD∥BC,AB=BC,对角线 AC、BD 交于点 O,BD 平分∠ABC,过点 D 作 DE⊥BC 交 BC 的延长线于点 E.连接 OE.
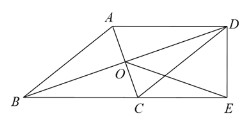
(1)求证:四边形 ABCD 是菱形;
(2)若 tan∠DBC=![]() ,AB=
,AB=![]() ,求线段 OE 的长.
,求线段 OE 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com