
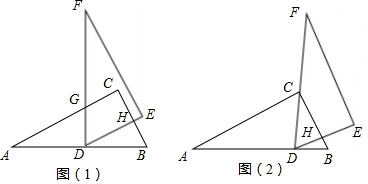
分析 (1)根据全等三角形的性质得到∠EDF=∠B,根据勾股定理得到AB=DF=10,根据三角形的中位线的性质得到DH=$\frac{1}{2}$AC=4,BH=CH=$\frac{1}{2}$BC=3,根据相似三角形的性质得到AG=$\frac{25}{4}$,CG=$\frac{7}{4}$,根据梯形的面积公式得到结论;
(2)如图(2),根据直角三角形的性质得到AD=BD=CD,由等腰三角形的性质得到∠ACD=∠A,根据余角的性质得到∠BCD=∠B,过H作HM⊥CD于M,由等腰三角形的性质得到DM=CM=$\frac{1}{2}$CD=$\frac{5}{2}$,根据相似三角形的性质得到DM=$\frac{10}{3}$,根据三角形的面积公式即可得到结论;
(3)边EF在绕点D旋转的过程中扫过了一个圆环,根据圆的面积公式得到结果.
解答 解:(1)在△ABC与△DEF中,$\left\{\begin{array}{l}{BC=DE}\\{∠ACB=∠DEF}\\{AC=EF}\end{array}\right.$,
∴△ABC≌△DEF,
∴∠EDF=∠B,
∵∠ACB=∠E=90°,
∴AB=DF=10,
∵DF⊥AB,
∴∠EDF+∠BDE=90°,
∴∠BDE=∠A,
∴DH∥AC,
∵AD=BD,
∴DH=$\frac{1}{2}$AC=4,BH=CH=$\frac{1}{2}$BC=3,
∵∠ADG=∠C=90°,∠A=∠A,
∴△ADG∽△ABC,
∴$\frac{AG}{AB}=\frac{AD}{AC}$,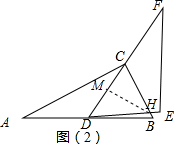
∴AG=$\frac{25}{4}$,
∴CG=$\frac{7}{4}$,
∴四边形DHCG的面积=$\frac{1}{2}$(4+$\frac{7}{4}$)×3=$\frac{69}{8}$,
(2)如图(2),
∵∠ACB=90°,D是AB的中点,
∴AD=BD=CD,
∴∠ACD=∠A,
∵∠A+∠B=∠ACD+∠BCD=90°,
∴∠BCD=∠B,
∵∠CDH=∠B,
∴∠CDH=∠DCH,
∴CH=DH,
过H作HM⊥CD于M,
则DM=CM=$\frac{1}{2}$CD=$\frac{5}{2}$,
∵∠HMD=∠ACB=90°,∠MDH=∠B,
∴△MDH∽△ABC,
∴$\frac{DM}{BC}=\frac{HM}{AC}$,即$\frac{\frac{5}{2}}{6}=\frac{MH}{8}$,
∴DM=$\frac{10}{3}$,
∴S△CDH=$\frac{1}{2}$×5×$\frac{10}{3}$=$\frac{25}{3}$;
(3)边EF在绕点D旋转的过程中扫过了一个圆环,
S圆环=102π-62π=64π,
故答案为:圆环,64π.
点评 本题考查了全等三角形的性质和判定、相似三角形的判定和性质、直角三角形斜边上的中线性质以及勾股定理和三角形面积和圆的面积的计算方法;本题难度较大,综合性强,培养学生综合运用定理进行推理论证和计算的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com