练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．已知关于x的一元二次方程x2-kx-2=0，
    （1）求证无论k为何值，方程总有两个不相等的实数根？
    （2）给k取一个你喜欢的值，并求解这个方程．

    分析 （1）根据方程各项的系数结合根的判别式即可得出△=k2+8≥8，由此可得出无论k为何值，方程总有两个不相等的实数根；
    （2）将k=1代入原方程中，再用分解因式法解方程即可得出结论．

    解答 （1）证明：在方程x2-kx-2=0中，
    △=（-k）2-4×1×（-2）=k2+8≥8，
    ∴无论k为何值，方程总有两个不相等的实数根；
    （2）解：当k=1时，方程为x2-x-2=（x+1）（x-2）=0，
    解得：x1=-1，x2=2．

    点评 本题考查了根的判别式以及解一元二次方程，根据根的判别式△=k2+8的符号确定方程解的情况是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

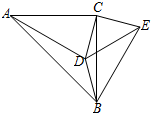    10．如图，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，CE⊥CD，且CE=CD，连接BD、DE、BE，则下列结论：①∠ECA=165°，②BE=BC；③AD=BE；④CD=BD．其中正确的是（　　）
    A．①②③B．①②④C．①③④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

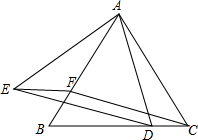    11．如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF．
    （1）求证：△ACD≌△CBF；
    （2）以AD为边作等边三角形△ADE，点D在线段BC上的何处时，四边形CDEF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知关于x的一元二次方程x2+（2m+3）x+m2=0有两个不相等的实数根，
    （1）求m的取值范围
    （2）若α，β是方程的两个实数根，且满足$\frac{1}{α}$+$\frac{1}{β}$=-1，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知：如图，点E是线段AB的中点，∠A=∠B，∠AED=∠BEC．求证：CE=DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．若一个正多边形的周长为48cm，且它的内角和为720°，求这个正多边形的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．为了增强学生体质，学校鼓励学生多参加体育锻炼，小胖同学马上行动，每天围绕小区进行晨跑锻炼．该小区外围道路近似为如图所示四边形ABCD，已知四边形ABED是正方形，∠DCE=45°，AB=100米．小胖同学某天绕该道路晨跑5圈，时间约为20分钟，求小胖同学该天晨跑的平均速度约为多少米/分？（结果保留整数，$\sqrt{2}$≈1.41）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解一元二次方程：
    （1）用配方法解：x2-4x-5=0      
    （2）用公式法解：x2-3x-1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．若x=-1是关于x的一元二次方程x2+3x+m+1=0的一个解，则m的值为1，另一个解是-2．

    查看答案和解析>>

    同步练习册答案