
【题目】已知:如图等边△ABC,D是AC的中点,E在BC的延长线上,且CE=CD,过D作DF⊥BE于点E.
(Ⅰ)求证:△BDE为等腰三角形;
(Ⅱ)请猜想FC与BF间的数量关系,并证明.

【答案】(Ⅰ)见解析;(Ⅱ)BF=3FC,理由见解析.
【解析】
(Ⅰ)根据“三线合一”得到∠ABD=∠CBD=30°,然后再由CE=CD,根据“等边对等角”得到∠CDE=∠E,因为∠ACB为三角形DCE的外角,根据外角性质得到∠CDE=∠E=30°,进而利用等量代换得到∠DBE=∠E,根据“等角对等边”得到DB=DE;
(Ⅱ)解直角三角形求得BF=![]() DF,DF=
DF,DF=![]() FC,从而证得BF=3FC.
FC,从而证得BF=3FC.
(Ⅰ)证明∵BD是等边△ABC的中线,
∴BD平分∠ABC,
∴∠DBE=![]() ∠ABC=30°,
∠ABC=30°,
又∵CE=CD,
∴∠E=∠CDE,∠E=![]() ∠ACB=30°.
∠ACB=30°.
∴∠DBE=∠E,
∴DB=DE,
∴△BDE为等腰三角形;
(Ⅱ)猜想FC与BF间的数量关系为:BF=3FC,
证明:∵D是等边△ABC的边AC的中点,
∴BD⊥AC,∠DBC=![]() ∠ABC=30°,
∠ABC=30°,
∴BF=![]() DF,
DF,
∵DF⊥BE,∠DCF=60°,
∴DF=![]() FC,
FC,
∴BF=3FC.


科目:初中数学 来源: 题型:
【题目】如图①是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!

如图②是(a+b)n的三个展开式.结合上述两图之间的规律解题:
(1)请直接写出(a+b)4的展开式:(a+b)4= .
(2)请结合图②中的展开式计算下面的式:(x+2)3= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BD是对角线,∠ADB=90°,E、F分别为边AB、CD的中点.
(1)求证:四边形DEBF是菱形;
(2)若BE=4,∠DEB=120°,点M为BF的中点,当点P在BD边上运动时,则PF+PM的最小值为 ,并在图上标出此时点P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米.两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示:

(1)根据图象,直接写出y1,y2关于x的函数关系式;
(2)当x为何值时,两车相遇?
(3)甲、乙两地间有A、B两个加油站,相距280千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④4a﹣2b+c<0;⑤c﹣a>1.其中所有正确结论的序号是_____.
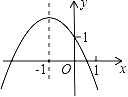
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0)、C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)设点M(3,n),求使MN+MD取最小值时n的值.
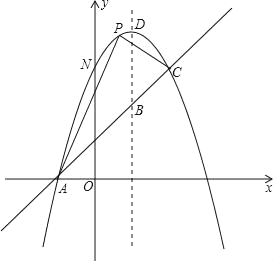
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com