
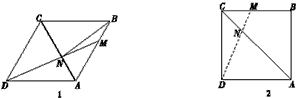
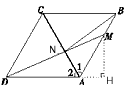
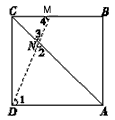
| 解:(1)①证明:∵四边形ABCD是菱形 ∴AB=AD,∠1=∠2 又∵AN=AN ∴△ABN≌△ADN ②作MH⊥DA交DA的延长线于点H,由AD∥BC,得∠MAH=∠ABC=60°, 在Rt△AMH中,MH=AM·sin60°=4×sin60°=2 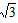 , ,∴点M到AD的距离为2 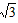 , ,易求AH=2,则DH=6+2=8 在Rt△DMH中,tan∠MDH= 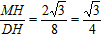 , ,由①知,∠MDH=∠ABN=α,故tanα= 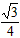 ; ; |
 |
| (2)∵∠ABC=90°, ∴菱形ABCD是正方形,此时,∠CAD=45°, 下面分三种情形: Ⅰ)若ND=NA,则∠ADN=∠NAD=45° 此时,点M恰好与点B重合,得x=6; Ⅱ)若DN=DA,则∠DNA=∠DAN=45° 此时,点M恰好与点C重合,得x=12; Ⅲ)若AN=AD=6,则∠1=∠2, 由AD∥BC,得∠1=∠4, 又∠2=∠3, ∴∠3=∠4,从而CM=CN, 易求AC=6 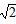 , ,∴CM=CN=AC-AN=6 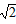 -6, -6,故x=12-CM=12-(6 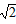 -6)=18-6 -6)=18-6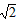 , ,综上所述:当x=6或12或18-6 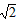 时,△ADN是等腰三角形。 时,△ADN是等腰三角形。 |
 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
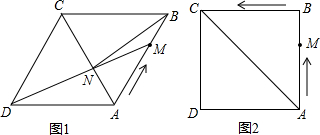 C的路线向终点C运动,连接DM交AC于点N,连接BN.
C的路线向终点C运动,连接DM交AC于点N,连接BN.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.
在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com