
如图,已知一次函数 (m为常数)的图象与反比例函数
(m为常数)的图象与反比例函数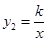 (k为常数,
(k为常数,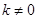 )的图象相交于点 A(1,3).
)的图象相交于点 A(1,3).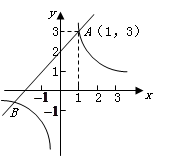
(1)求这两个函数的解析式及其图象的另一交点 的坐标;
的坐标;
(2)观察图象,写出使函数值 的自变量
的自变量 的取值范围.
的取值范围.
(1)一次函数解析式为:y1=x+2,B(﹣3,﹣1);
(2)根据图象得:函数值y1≥y2的自变量x的取值范围是:x≥1或﹣3≤x<0.
解析试题分析:(1)利用待定系数法把 A(1,3)代入一次函数y1=x+m与反比例函数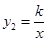 中,可解出m、k的值,进而可得解析式,求B点坐标,就是把两函数解析式联立,求出x、y的值;
中,可解出m、k的值,进而可得解析式,求B点坐标,就是把两函数解析式联立,求出x、y的值;
(2)根据函数图象可以直接写出答案.
试题解析:(1)∵一次函数y1=x+m(m为常数)的图象与反比例函数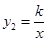 (k为常数,k≠0)的图象相交于点 A(1,3),
(k为常数,k≠0)的图象相交于点 A(1,3),
∴3=1+m,k=1×3,
∴m=2,k=3,
∴一次函数解析式为:y1=x+2,
反比例函数解析式为:y2=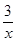 ,
,
由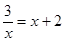 ,
,
解得:x1=﹣3,x2=1,
当x1=﹣3时,y1=﹣1,
x2=1时,y1=3,
∴两个函数的交点坐标是:A(1,3)和B(﹣3,﹣1)
∴B(﹣3,﹣1);
(2)根据图象得:函数值y1≥y2的自变量x的取值范围是:x≥1或﹣3≤x<0.
考点:反比例函数解析式,一次函数解析式,反比例函数的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
函数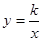 和
和 的图象关于y轴对称,我们定义函数
的图象关于y轴对称,我们定义函数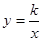 和
和 相互为“影像”函数。
相互为“影像”函数。
类似地,如果函数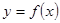 和
和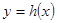 的图象关于y轴对称,那么我们定义函数
的图象关于y轴对称,那么我们定义函数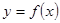 和
和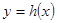 互为“影像”函数。
互为“影像”函数。
(1)请写出函数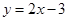 的“影像”函数: ;
的“影像”函数: ;
(2)函数 的“影像”函数是 ;
;
(3)如果,一条直线与一对“影像”函数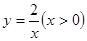 和
和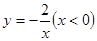 的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数
的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数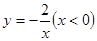 的“影像”函数上的对应点的横坐标是1,求点B的坐标。
的“影像”函数上的对应点的横坐标是1,求点B的坐标。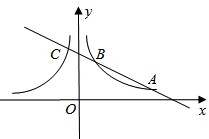
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为 m,DC的长为
m,DC的长为 m.
m.
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一次函数 的图像与反比例函数
的图像与反比例函数 的图象交于A(-2,1),B(1,n)两点.
的图象交于A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△OAB的面积.
(3)写出反比例函数值大于一次函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,反比例函数y=(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知正比例函数y=ax与反比例函数 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2).
(1)求这两个函数的表达式;
(2)画出草图,根据图象写出正比例函数值大于反比例函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知点O是平面直角坐标系的原点,直线y=﹣x+m+n与双曲线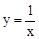 交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=的图象的两个交点.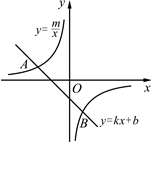
【小题1】求此反比例函数和一次函数的解析式
【小题2】根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com