
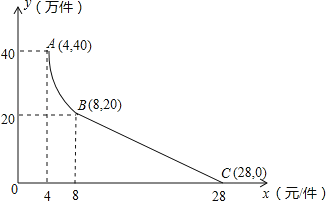
【题目】某公司用100万元研发一种市场急需电子产品,已于当年投入生产并销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,设公司销售这种电子产品的年利润为s(万元).
(1)请求出y(万件)与x(元/件)的函数表达式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)的函数表达式,并求出第一年年利润的最大值.
【答案】(1)y= ;(2)当每件的销售价格定为16元时,第一年年利润的最大值为44万元.
;(2)当每件的销售价格定为16元时,第一年年利润的最大值为44万元.
【解析】
(1)依据待定系数法,即可求出y(万件)与x(元/件)之间的函数关系式;
(2)分两种情况进行讨论,当x=8时,smax=﹣20;当x=16时,smax=44;根据44>﹣20,可得当每件的销售价格定为16元时,第一年年利润的最大值为44万元.
解:(1)当4≤x≤8时,设y=![]() ,将A(4,40)代入得k=4×40=160,
,将A(4,40)代入得k=4×40=160,
∴y与x之间的函数关系式为y=![]() ;
;
当8<x≤28时,设y=k'x+b,将B(8,20),C(28,0)代入得,
![]() ,
,
解得![]() ,
,
∴y与x之间的函数关系式为y=﹣x+28,
综上所述,y=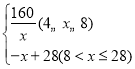 ;
;
(2)当4≤x≤8时,s=(x﹣4)y﹣160=(x﹣4)![]() ﹣100=
﹣100=![]() +60,
+60,
∵当4≤x≤8时,s随着x的增大而增大,
∴当x=8时,smax=![]() +60=﹣20;
+60=﹣20;
当8<x≤28时,s=(x﹣4)y﹣80=(x﹣4)(﹣x+28)﹣80=﹣(x﹣100)2+44,
∴当x=16时,smax=44;
∵44>﹣20,
∴当每件的销售价格定为16元时,第一年年利润的最大值为44万元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的延长线上一点,且∠PDB=
的延长线上一点,且∠PDB=![]() ∠A,连接
∠A,连接![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)填空:
①当![]() 的度数为______时,四边形
的度数为______时,四边形![]() 是菱形;
是菱形;
②当![]() 时,
时,![]() 的面积为_________.
的面积为_________.
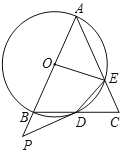
查看答案和解析>>
科目:初中数学 来源: 题型:
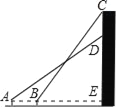
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(18)班开展数学活动,毓齐和博文两位同学合作用测角仪测量学校的旗杆,毓齐站在B点测得旗杆顶端E点的仰角为45°,博文站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知毓齐和博文相距(BD)30米,毓齐的身高(AB)1.6米,博文的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1)
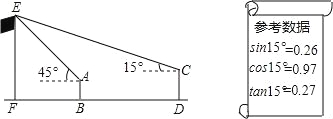
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,以OA2为斜边在△OA1A2外部作等腰直角△OA2A3,以OA3为斜边在△OA2A3外部作等腰直角△OA3A4,以OA4为斜边在△OA3A4外部作等腰直角△OA4A5,…,连接A1A3,A2A4,A3A5,…分别与OA2,OA3,OA4,交于点C1,C2,C3,按此规律继续下去,则△OAnCn的面积等于_____.(用含正整数n的式子表示)
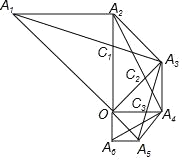
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个,小明将球搅匀后从中摸出一个球是红球的概率是0.25.
(1)求口袋中红球的个数;
(2)若小明第一次从中摸出一个球,放回搅匀后再摸出一个球,请通过树状图或者列表的方法求出小明两次均摸出红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于点C1交AB的延长线于点B1.
(1)请你探究:![]() =
=![]() ,
,![]() =
=![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() =
=![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)如图(2)所示Rt△ABC中,∠ACB=90°,AC=8,AB=![]() ,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求
,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求![]() 的值.
的值.
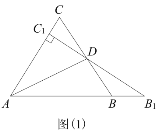
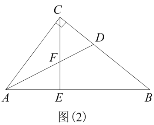
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com