

���� ��2���ٽ��ۣ�PD-DQ=AB����ͼ���У��ӳ�CA��M��ʹ��AM=AP������PM��ֻҪ֤����PAM�ǵȱ������Σ���PCM�ա�PQD���ɽ�����⣻
�ڽ��ۣ�DQ-PD=AB����ͼ���У���DQ�Ͻ�ȡDM=DP������PM��ֻҪ֤����PDM�ǵȱ������Σ���PCM�ա�PQD���ɽ�����⣻
��� �⣺��2���ٽ��ۣ�PD-DQ=AB��
���ɣ���ͼ���У��ӳ�CA��M��ʹ��AM=AP������PM��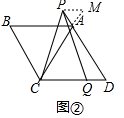
���ı���ABCD�����Σ���B=60�㣬
���ABC����ACD���ǵȱ������Σ�
���CAD=��PAM=60�㣬
���PAM�ǵȱ������Σ�
��AM=PM����M=��ACD=60�㣬
��PM��CD��
���PCD+��CPM=180�㣬
��PC=PQ��
���PCQ=��PQC��
�ߡ�PQC+��PQD=180�㣬
���CPM=��PQD��
���PCM�ա�PQD��
��CM=PD��PM=QD=AM��
��CM=AC+AM=AB+QD��
��PD-DQ=AB��
�ڽ��ۣ�DQ-PD=AB��
���ɣ���ͼ���У���DQ�Ͻ�ȡDM=DP������PM��
�ߡ�B=��ADC=120�㣬
���PDM=60�㣬��DP=DM��
���PDM�ǵȱ������Σ�
��PD=PM����PMC=��PDQ=60�㣬
��PC=PQ��
���PCM=��Q��
���PCM�ա�PQD��
��CM=DQ��
��CD+DM=DQ��
��AB+PD=DQ��
��DQ-PD=AB��
���� ���⿼���ı����ۺ��⡢���ε����ʡ��ȱ������ε����ʺ��ж���ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п�ѹ���⣮


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ���� | Ƶ�� |
| 25��x��30 |  | 4 |
| 30��x��35 | ������ | 15 |
| 35��x��40 | ������������һ | 31 |
| 40��x��45 | ��һ | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
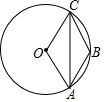 ��ͼ���뾶Ϊ3cm�ġ�O�ϣ�������A��B��C�����㣬���ı���OABCΪ���Σ�����AC���ԵĻ���Ϊ2�л�4��cm��
��ͼ���뾶Ϊ3cm�ġ�O�ϣ�������A��B��C�����㣬���ı���OABCΪ���Σ�����AC���ԵĻ���Ϊ2�л�4��cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
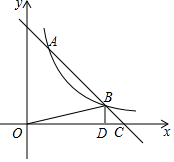 ��ͼ��ֱ��y=-x+5��˫����y=$\frac{k}{x}$��x��0���ཻ��A��B���㣬��x�ύ�ڵ�C������B��BD��x���ڵ�D����BDC�������$\frac{1}{2}$����k��ֵΪ��������
��ͼ��ֱ��y=-x+5��˫����y=$\frac{k}{x}$��x��0���ཻ��A��B���㣬��x�ύ�ڵ�C������B��BD��x���ڵ�D����BDC�������$\frac{1}{2}$����k��ֵΪ��������| A�� | 3.5 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
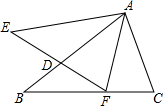 ��ͼ����ABC���AEF�У�AB=AE��BC=EF����B=��E��AB��EF��D���������н��ۣ�
��ͼ����ABC���AEF�У�AB=AE��BC=EF����B=��E��AB��EF��D���������н��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90�㣬��ACΪֱ���ġ�O��AB�߽��ڵ�D������D�����߽�BC�ڵ�E��
��ͼ����Rt��ABC�У���ACB=90�㣬��ACΪֱ���ġ�O��AB�߽��ڵ�D������D�����߽�BC�ڵ�E���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com