
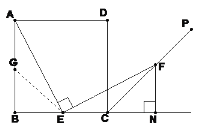
【题目】如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y。
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.

【答案】(1)AE=EF;(2)①y=-![]() x2+2x(0<x<4),②当x=2,y最大值=2.
x2+2x(0<x<4),②当x=2,y最大值=2.
【解析】
(1)在AB上取一点G,使AG=EC,连接GE,利用ASA,易证得:△AGE≌△ECF,则可证得:AE=EF;
(2)同(1)可证明AE=EF,利用AAS证明△ABE≌△ENF,根据全等三角形对应边相等可得FN=BE,再表示出EC,然后利用三角形的面积公式即可列式表示出△ECF的面积为y,然后整理再根据二次函数求解最值问题.
(1)如图,在AB上取AG=EC,
∵四边形ABCD是正方形,
∴AB=BC,
有∵AG=EC ,∴BG=BE ,
又∵∠B=90°,
∴∠AGE=135°,
又∵∠BCD=90°,CP平分∠DCN,
∴∠ECF=135°,
∵∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AGE和△ECF中,
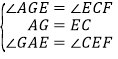 ,
,
∴△AGE≌△ECF,
∴AE=EF;
(2)①∵由(1)证明可知当E不是中点时同理可证AE=EF,
∵∠BAE=∠NEF,∠B=∠ENF=90°,
∴△ABE≌△ENF,
∴FN=BE=x,
∴S△ECF=![]() (BC-BE)·FN,
(BC-BE)·FN,
即y=![]() x(4-x),
x(4-x),
∴y=- ![]() x2+2x(0<x<4),
x2+2x(0<x<4),
②![]() ,
,
当x=2,y最大值=2.


科目:初中数学 来源: 题型:
【题目】![]() 和△A′B′C′在平面直角坐标系中的位置分别如图所示.
和△A′B′C′在平面直角坐标系中的位置分别如图所示.
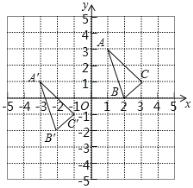
(1)分别写出下列各点的坐标:A ;B ;C ;
(2)△A′B′C′由 ![]() 经过怎样的平移得到?并写出点A′,B′,C′的坐标.
经过怎样的平移得到?并写出点A′,B′,C′的坐标.
(3)求![]() 面积.
面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于![]() 的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( )
的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( )

A.100°B.110°C.120°D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).用列表法或树形图表示出(x,y)的所用可能出现的结果;求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现
探索:如图,在直角坐标系中,正方形ABCO的点B坐标(4,4),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.

(1)证明:BE=DE.
小明给出的思路为:过E作y轴的平行线交AB、x轴于点F、H.请完善小明的证明过程.
(2)若点D坐标为(3,0),则点E坐标为 .
若点D坐标为(a,0),则点E坐标为 .
发现:在直角坐标系中,点B坐标(5,3),点D坐标(3,0),找一点E,使得△BDE为等腰直角三角形,直接写出点E坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点分别为A(2,4),B(﹣2,2),C(3,1).
(1)作出△ABC关于x轴对称的图形△DEF,写出顶点D、E、F的坐标.
(2)如果点H(3m﹣1,n﹣6)与点H′(2n+7,3m﹣9)关于y轴对称,求m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条抛物线的开口大小与方向、对称轴均与抛物线y=![]() x2相同,并且抛物线经过点(1,1).
x2相同,并且抛物线经过点(1,1).
(1)求抛物线的解析式,并指明其顶点;
(2)所求抛物线如何由抛物线y=![]() x2平移得到?
x2平移得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com