
 如图,已知矩形ABCD(AB<AD).
如图,已知矩形ABCD(AB<AD).分析 (1)根据题目要求作图即可;
(2)由(1)知AE=AD=10、∠DAF=∠EAF,可证△DAF≌△EAF得∠D=∠AEF=90°,即可得∠FEC=∠BAE,从而由tan∠FEC=tan∠BAE=$\frac{BE}{AB}$可得答案.
解答 解:(1)如图所示;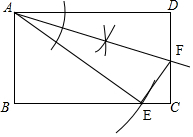
(2)由(1)知AE=AD=10、∠DAF=∠EAF,
∵AB=8,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=6,
在△DAF和△EAF中,
∵$\left\{\begin{array}{l}{AD=AE}\\{∠DAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△DAF≌△EAF(SAS),
∴∠D=∠AEF=90°,
∴∠BEA+∠FEC=90°,
又∵∠BEA+∠BAE=90°,
∴∠FEC=∠BAE,
∴tan∠FEC=tan∠BAE=$\frac{BE}{AB}$=$\frac{6}{8}$=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题主要考查作图-基本作图及全等三角形的判定与性质、解直角三角形,熟练掌握角平分线的尺规作图和全等三角形的判定与性质是解题的关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2x2+1 | B. | y=2x2-3 | C. | y=2(x-8)2+1 | D. | y=2(x-8)2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,2 | B. | 2,3 | C. | 2,2 | D. | 3,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
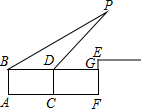 某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下:
某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com