
【题目】在平面直角坐标系中,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 如图摆放,边
如图摆放,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿
出发沿![]() 轴正方向滑动.
轴正方向滑动.
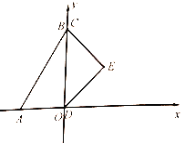
![]() 设点
设点![]() 关于
关于![]() 的函数表达式为________.
的函数表达式为________.
![]() 连接
连接![]() .当点
.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,
时,![]() 的面积最大值为_______.
的面积最大值为_______.
【答案】y=x ![]()
【解析】
(1)根据题意,判定点E在DE所在的直线上运动,即可得出函数表达式;
(2)首先判定点E的运动轨迹,当E′F⊥DF时,![]() 的面积最大,然后利用等腰直角三角形以及解直角三角形,即可得出E′F,进而得出△AOE面积.
的面积最大,然后利用等腰直角三角形以及解直角三角形,即可得出E′F,进而得出△AOE面积.
(1)由题意,得当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿
出发沿![]() 轴正方向滑动时,点E在DE所在的直线上运动,
轴正方向滑动时,点E在DE所在的直线上运动,
∵CDE为![]() 角的三角板
角的三角板
∴![]() 关于
关于![]() 的函数表达式为
的函数表达式为![]() ;
;
(2)当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,点E的运动轨迹为E-E′-E,当E′F⊥DF时,
时,点E的运动轨迹为E-E′-E,当E′F⊥DF时,![]() 的面积最大,如图所示:
的面积最大,如图所示:
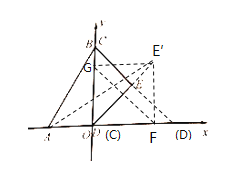
由(1)知,∠E′DF=45°
∴四边形GOFE′为正方形
∴△COE≌△GFE′
∴OE′=OC
∵∠ABO=30°,![]()
∴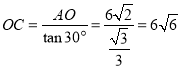
∴![]()
∴![]() 的面积为
的面积为![]()
故答案为:![]() ;
;![]() .
.


科目:初中数学 来源: 题型:
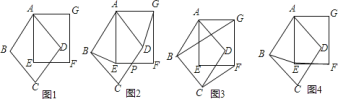
【题目】我们给定两个全等的正方形![]() 、
、![]() ,它们共顶点
,它们共顶点![]() (如图
(如图![]() ),可以绕顶点
),可以绕顶点![]() 旋转,
旋转,![]() ,
,![]() 相交于点
相交于点![]() ,以下各问题都以此为前提.
,以下各问题都以此为前提.
问题要求:
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),求证:
),求证:![]() ,
,![]() ;
;
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),有三个结论:
),有三个结论:
①![]() ;
;
②![]() ;
;
③![]() 与
与![]() 位似.
位似.
请你从①,②,③三个结论中选择一个进行证明:
(说明:选①做对的得![]() 分,选②做对的得
分,选②做对的得![]() 分,选③做对的得
分,选③做对的得![]() 分)
分)
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),求
),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,Q是⊙P上的一个动点.
(1)在图中标出圆心P位置,写出点P坐标;
(2)Q点在圆上坐标为何值时,△ABQ是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
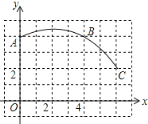
【题目】如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;
(2)请在(1)的基础上,完成下列填空:⊙D的半径为__________;点(6,–2)在⊙D__________;(填“上”、“内”、“外”)∠ADC的度数为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() 交
交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,平行于
两点,平行于![]() 轴的直线
轴的直线![]() 从点
从点![]() 开始以每秒
开始以每秒![]() 个单位的速度向
个单位的速度向![]() 轴的负方向运动,直线
轴的负方向运动,直线![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设直线
,设直线![]() 的运动时间为
的运动时间为![]() 秒.
秒.

![]() 求线段
求线段![]() 的长.
的长.
![]() 若
若![]() 为直线
为直线![]() 上一动点,将
上一动点,将![]() 沿着
沿着![]() 翻折,当点
翻折,当点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上时,求直线
上时,求直线![]() 的解析式.
的解析式.
![]() 若
若![]() 为
为![]() 的中点,当
的中点,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
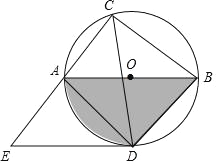
【题目】如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的阴影部分的面积是 ;
围成的阴影部分的面积是 ;
(2)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
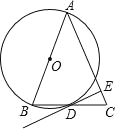
【题目】如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.
(1)求证:BD=CD;
(2)若AB=3,cos∠ABC=![]() ,在腰AC上取一点E使AE=
,在腰AC上取一点E使AE=![]() ,试判断DE与⊙O的位置关系,并证明.
,试判断DE与⊙O的位置关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com