
 如图所示,矩形ABCD的面积为36平方厘米,四边形PMON的面积是3平方厘米,则阴影部分的面积是12平方厘米.
如图所示,矩形ABCD的面积为36平方厘米,四边形PMON的面积是3平方厘米,则阴影部分的面积是12平方厘米. 分析 阴影部分的面积=△AOD的面积+△BOC的面积-(△AOM的面积+△BON的面积)即可.由等底等高的三角形面积相等,得出△AOD的面积+△BOC的面积=$\frac{1}{2}$平行四边形ABCD的面积=18平方厘米,△AOM面积+△BON的面积=△ABP的面积-△AOB的面积-四边形PMON的面积,即可得出结果.
解答 解:∵△ABP的面积=$\frac{1}{2}$平行四边形ABCD的面积=18(平方厘米);
△AOB的面积=$\frac{1}{2}$△ABC的面积=$\frac{1}{2}$平行四边形ABCD的面积=36×$\frac{1}{4}$=9(平方厘米);
又∵四边形PMON的面积=3平方厘米,
∴△AOM的面积+△BON的面积
=△ABP的面积-△AOB的面积-四边形PMON的面积
=18-9-3
=6(平方厘米);
∴阴影部分的面积=△AOD的面积+△BOC的面积-(△AOM的面积+△BON的面积)
=$\frac{1}{2}$平行四边形ABCD的面积-6
=18-6
=12(平方厘米);
答:阴影部分的面积为12平方厘米.
故答案为:12.
点评 此题考查了矩形的性质,重点考查学生对组合图形的分析以及对面积的计算能力,以及对“等底等高的三角形面积相等”这一知识的掌握与运用情况.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )
如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )| A. | 这天15时温度最高 | |
| B. | 这天3时温度最低 | |
| C. | 这天最高温度与最低温度的差是13℃ | |
| D. | 这天0-3时,15-24时温度在下降 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
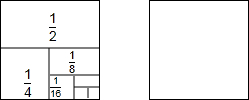 (1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.
(1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
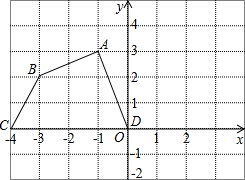 如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0)
如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com