
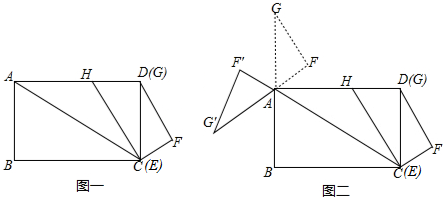
���� ��1����ͼ1��ֱ�����ù��ɶ�����CD�ij�����֤����CDF�ס�HCD����$\frac{CF}{HD}=\frac{DF}{CD}$����������HD�ij�����AD=AH+DH=$\frac{5}{2}\sqrt{5}$+$\frac{3}{2}\sqrt{5}$=4$\sqrt{5}$�����ù��ɶ�����AC��
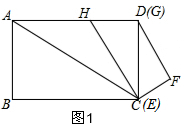
��2���ȼ���ƽ�ƹ����е�����λ�ã���GE������Hʱ����ͼ2����EC�ij�����ʱ��t=$\frac{15\sqrt{5}}{8}$$��\sqrt{5}$=$\frac{15}{8}$����FG��ֱ��CH��ʱ���������Ǻ�����ʽ��EC����ͼ3����ʱ��t=$\frac{15\sqrt{5}}{8}$$��\sqrt{5}$=$\frac{15}{8}$������F�ڱ�AD��ʱ����ͼ4�������������FM�ij������ù��ɶ�����EM�ij����ٸ������Ǻ�����ʽ��EC����ʱ��t=4$\sqrt{5}$��$\sqrt{5}$=4��
�����������
�ٵ�0��t��$\frac{15}{8}$ʱ����ͼ5���ص�������ֱ�ǡ�EMN�����������Ǻ�����EN������MN�����������ʽ��S��
�ڵ�$\frac{15}{8}$��t��3ʱ����ͼ6���ص��������ı���NEMH��������������ϵʽ��
�۵�3��t��4ʱ����ͼ7���ص��������ı���NEFM��������������ϵʽ��
�ܵ�4��t��5ʱ����ͼ8���ص�������ֱ�ǡ�EMN�����ݹ�ʽ�����������
��3�����ڣ������������
�ٵ�AQ=APʱ����ͼ9���ڵ�AQ=PQʱ����ͼ10���۵�AQ=APʱ����ͼ11���ܵ�AP=AQʱ����ͼ12��
����Q��QN��AD����DA���ӳ�����N���������Ǻ�����ʽ���������ӦAQ�ij���
���  �⣺��1����ͼ1��Rt��EFG�У���F=90�㣬
�⣺��1����ͼ1��Rt��EFG�У���F=90�㣬
�ɹ��ɶ����ã�CD=$\sqrt{C{F}^{2}+D{F}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$��
���ı���ABCDΪ���Σ�
���ADC=90�㣬
���ADC=��DFC=90�㣬
��CHƽ�֡�ACD��
�ߡ�ACD=2��DCH��
�ߡ�ACD=2��EGF��
���DCH=��EGF��
���CDF�ס�HCD��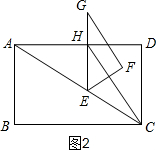
��$\frac{CF}{HD}=\frac{DF}{CD}$��
��$\frac{3}{HD}=\frac{6}{3\sqrt{5}}$��
��HD=$\frac{3}{2}\sqrt{5}$��
��AD=AH+DH=$\frac{5}{2}\sqrt{5}$+$\frac{3}{2}\sqrt{5}$=4$\sqrt{5}$��
��Rt��ACD��AD=4$\sqrt{5}$��CD=3$\sqrt{5}$��
��AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{��4\sqrt{5}��^{2}+��3\sqrt{5}��^{2}}$=5$\sqrt{5}$��
��2����GE������Hʱ����ͼ2��
��GE��BC��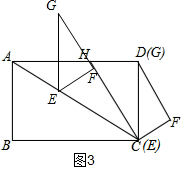
��GE��AD��
��Rt��AHE��cos��DAC=$\frac{AH}{AE}=\frac{AD}{AC}$��
��$\frac{\frac{5}{2}\sqrt{5}}{AE}=\frac{4\sqrt{5}}{5\sqrt{5}}$=$\frac{4}{5}$��
��AE=$\frac{25\sqrt{5}}{8}$��
��CE=5$\sqrt{5}$-$\frac{25\sqrt{5}}{8}$=$\frac{15\sqrt{5}}{8}$��
��ʱ��t=$\frac{15\sqrt{5}}{8}$$��\sqrt{5}$=$\frac{15}{8}$��
��FG��ֱ��CH��ʱ����ͼ3��
Rt��EFC��sin��ACH=sin��CDF=$\frac{EF}{CD}=\frac{EF}{CE}$��
��CD=CE=3$\sqrt{5}$��
��ʱ��t=3$\sqrt{5}$��$\sqrt{5}$=3��
����F�ڱ�AD��ʱ����ͼ4��
S��GEF=$\frac{1}{2}$EF•FG=$\frac{1}{2}$EG•FM��
3��6=3$\sqrt{5}$•FM��
FM=$\frac{6\sqrt{5}}{5}$��
�ɹ��ɶ����ã�EM=$\sqrt{E{F}^{2}-F{M}^{2}}$=$\sqrt{{3}^{2}-��\frac{6\sqrt{5}}{5}��^{2}}$=$\frac{3\sqrt{5}}{5}$��
sin��DAC=$\frac{EM}{AE}=\frac{3}{5}$��
$\frac{\frac{3\sqrt{5}}{5}}{AE}$=$\frac{3}{5}$��AE=$\sqrt{5}$��
��EC=5$\sqrt{5}$-$\sqrt{5}$=4$\sqrt{5}$��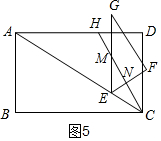
��ʱ��t=4$\sqrt{5}$��$\sqrt{5}$=4��
�����������
�ٵ�0��t��$\frac{15}{8}$ʱ����ͼ5���ص�������ֱ�ǡ�EMN��
������ã�CE=$\sqrt{5}$t��
��MN��FG��
���ENM=��EFG=90�㣬
sin��ACH=sin��EGF=$\frac{EN}{EC}=\frac{EF}{EG}$��
$\frac{EN}{\sqrt{5}t}=\frac{3}{3\sqrt{5}}$��
EN=t��
��HC��FG��
���EMN=��G��
tan��EMN=tan��G=$\frac{EN}{MN}=\frac{EF}{FG}$��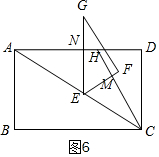
��$\frac{t}{MN}=\frac{3}{6}$��
��MN=2t��
��S=S��EMN=$\frac{1}{2}$EN•MN=$\frac{1}{2}$t•2t=t2��
�ڵ�$\frac{15}{8}$��t��3ʱ����ͼ6���ص��������ı���NEMH��
ͬ���ã�EM=t��CM=2t��
��AE=5$\sqrt{5}$-$\sqrt{5}$t��
��EN��CD��
���ANE�ס�ADC��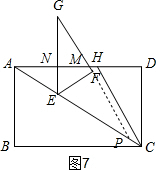
��$\frac{AN}{AD}=\frac{EN}{CD}=\frac{AE}{AC}$��
��$\frac{AN}{4\sqrt{5}}$=$\frac{EN}{3\sqrt{5}}$=$\frac{5\sqrt{5}-\sqrt{5}t}{5\sqrt{5}}$��
��AN=$\frac{4\sqrt{5}��5-t��}{5}$��EN=$\frac{3\sqrt{5}��5-t��}{5}$��
��S=S��AHC-S��AEN-S��EMC��
=$\frac{1}{2}$AH•CD-$\frac{1}{2}$AN•EN-$\frac{1}{2}$EM•MC��
=$\frac{1}{2}$��$\frac{5}{2}\sqrt{5}$��$3\sqrt{5}$-$\frac{1}{2}$��$\frac{4\sqrt{5}��5-t��}{5}$��$\frac{3\sqrt{5}��5-t��}{5}$-$\frac{1}{2}$t•2t��
=-$\frac{11}{5}{t}^{2}$+12t-$\frac{45}{4}$��
�۵�3��t��4ʱ����ͼ7���ص��������ı���NEFM��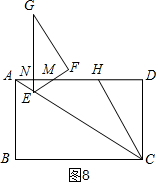 �ӳ�GF��AC��P��
�ӳ�GF��AC��P��
��GF��CH��
��sin��GPE=sin��HCA=$\frac{EF}{EP}=\frac{3}{3\sqrt{5}}$��
��$\frac{3}{EP}=\frac{3}{3\sqrt{5}}$��
��EP=3$\sqrt{5}$��
��PM��CH��
���APM�ס�ACH��
��$\frac{AP}{AC}=\frac{AM}{AH}$��
��$\frac{5\sqrt{5}-\sqrt{5}t+3\sqrt{5}}{5\sqrt{5}}$=$\frac{AM}{\frac{5}{2}\sqrt{5}}$��
��AM=$\frac{\sqrt{5}}{2}$��8-t����
��MN=AM-AN=$\frac{\sqrt{5}}{2}��8-t��$-$\frac{4\sqrt{5}��5-t��}{5}$=$\frac{3\sqrt{5}}{10}t$��
��GN=2MN=$\frac{3\sqrt{5}}{5}$t��
��S=S��GEF-S��GMN=$\frac{1}{2}$EF•FG-$\frac{1}{2}$MN•GN=$\frac{1}{2}$��3��6-$\frac{1}{2}$��$\frac{3\sqrt{5}}{10}t$��$\frac{3\sqrt{5}}{5}t$=-$\frac{9}{20}{t}^{2}$+9��
�ܵ�4��t��5ʱ����ͼ8���ص�������ֱ�ǡ�EMN��
�ɢڵã�EN=$\frac{3\sqrt{5}��5-t��}{5}$��
tan��GEF=$\frac{MN}{EN}=\frac{6}{3}$=2��
��MN=2EN=$\frac{6\sqrt{5}��5-t��}{5}$��
��S=S��EMN=$\frac{1}{2}$EN•MN=$\frac{1}{2}$•$\frac{3\sqrt{5}��5-t��}{5}$•$\frac{6\sqrt{5}��5-t��}{5}$=$\frac{9}{5}{t}^{2}$-18t+45��
����������S=$\left\{\begin{array}{l}{{t}^{2}��0��t��\frac{15}{8}��}\\{-\frac{11}{5}{t}^{2}+12t-\frac{45}{4}��\frac{15}{8}��t��3��}\\{-\frac{9}{20}{t}^{2}+9��3��t��4��}\\{\frac{9}{5}{t}^{2}-18t+45��4��t��5��}\end{array}\right.$��
��3�����ڣ�
�����������
�ٵ�AQ=APʱ����ͼ9��
��Q��QN��AD����DA���ӳ�����N��
��AF���PQ��
��F��Q=F��P��
tan��CAD=tan��NAQ=$\frac{CD}{AD}=\frac{NQ}{AN}$=$\frac{3\sqrt{5}}{4\sqrt{5}}$=$\frac{3}{4}$��
��NQ=3x��AN=4x����AQ=AP=5x��
��PN=9x��
tan��F��PA=$\frac{AF��}{F��P}=\frac{NQ}{PN}$��
��$\frac{3}{F��P}=\frac{3x}{9x}=\frac{1}{3}$��
��F��P=9��
��F��Q=F��P=9��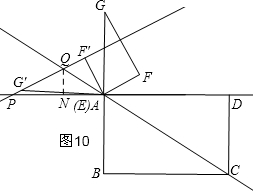
��AQ=$\sqrt{F��{A}^{2}+F��{Q}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$��
�ڵ�AQ=PQʱ����ͼ10��
��Q��QN��AD����DA���ӳ�����N��
���F��PN=��QAP��
��tan��F��PN=tan��DAC=$\frac{AF��}{PF��}=\frac{DC}{AD}=\frac{3}{4}$��
��$\frac{3}{F��P}=\frac{3}{4}$��
��F��P=4��
��AQ=x����PQ=x��QF��=4-x��
�ɹ��ɶ����ã�x2=32+��4-x��2��
��ã�x=$\frac{25}{8}$��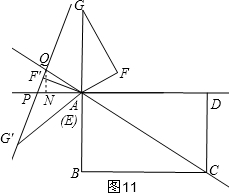
��AQ=$\frac{25}{8}$��
�۵�AQ=APʱ����ͼ11��
��Q��QN��AD����DA���ӳ�����N��
ͬ����QN=3x��AN=4x��AQ=AP=5x��
��PN=x��
��PQ=$\sqrt{Q{N}^{2}+P{N}^{2}}$=$\sqrt{��3x��^{2}+{x}^{2}}$=$\sqrt{10}x$��
��AP=AQ��AF���PQ��
��PF��=F��Q=$\frac{\sqrt{10}}{2}x$��
Rt��AF��Q��AQ2=F��A2+F��Q2��
��$��5x��^{2}={3}^{2}+��\frac{\sqrt{10}}{2}x��^{2}$��
x=��$\frac{\sqrt{10}}{5}$��
��AQ=5x=$\sqrt{10}$��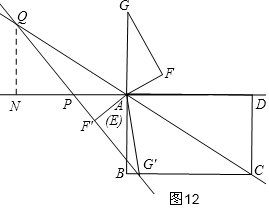
�ܵ�AP=AQʱ����ͼ12��
��Q��QN��AD����DA���ӳ�����N��
��AP=AQ����QNP=��AF��P=90�㣬��QPN=��F��PA��
�����QNP�ա�QF��P��
��AF��=QN=3��
sin��QAN=sin��DAC=$\frac{3}{5}$=$\frac{NQ}{AQ}$��
��AQ=5��
����������AQ�ij�Ϊ3$\sqrt{10}$��$\frac{25}{8}$��$\sqrt{10}$��5��
���� �������ı��ε��ۺ��⣬�Ƚϸ��ӣ������˾��Ρ����������ε����ʺ�ֱ�������εļ��α任���⣬�뺯�����ϣ����������ʽ�����Ǻ��������ɶ����е�����ϵʽ����ʾS��t�ĺ�����ϵʽ��ͬʱ�����˷������۵�˼�룬���������⣬Ҫע�����ν�ϣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ȵ��������ǵȻ� | B�� | ��Բ�ǻ� | ||
| C�� | ����ֱ�� | D�� | ͬ��Բ�ǵ�Բ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com