
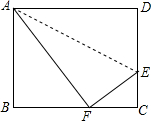
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=$\frac{3}{4}$,那么矩形ABCD的周长为36cm.
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=$\frac{3}{4}$,那么矩形ABCD的周长为36cm. 分析 根据tan∠EFC的值,可设CE=3k,在Rt△EFC中可得CF=4k,EF=DE=5k,根据∠BAF=∠EFC,利用三角函数的知识求出AF,然后在Rt△AEF中利用勾股定理求出k,继而代入可得出答案.
解答 解:∵tan∠EFC=$\frac{3}{4}$,
∴设CE=3k,则CF=4k,
由勾股定理得EF=DE=5k,
∴DC=AB=8k,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=tan∠EFC=$\frac{3}{4}$,
∴BF=6k,AF=BC=AD=10k,
在Rt△AFE中由勾股定理得AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{125{k}^{2}}$=5$\sqrt{5}$,
解得:k=1,
故矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36cm,
故答案为:36.
点评 此题考查了矩形的性质以及翻折变换的知识,解答本题关键是根据三角函数值,表示出每条线段的长度,然后利用勾股定理进行解答,有一定难度.


科目:初中数学 来源: 题型:解答题
 随着科技的发展,电动汽车的性能得到显著提高.某市对市场上电动汽车的性能进行随机抽样调查,抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据,绘制成如下两幅表和图.
随着科技的发展,电动汽车的性能得到显著提高.某市对市场上电动汽车的性能进行随机抽样调查,抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据,绘制成如下两幅表和图.| 组别 | 行驶的里程x(千米) | 频数(台) | 频率 |
| A | x<200 | 18 | 0.15 |
| B | 200≤x<210 | 36 | a |
| C | 210≤x<220 | 30 | |
| D | 220≤x<230 | b | |
| E | x≥230 | 12 | 0.10 |
| 合计 | c | 1.00 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于C、D两点,和x轴交于A点,y轴交于B点.已知点C的坐标为(3,6),CD=2BC.
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于C、D两点,和x轴交于A点,y轴交于B点.已知点C的坐标为(3,6),CD=2BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
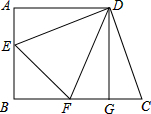 如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF.
如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由a>b,得a-2<b-2 | B. | 由a>b,得|a|>|b| | C. | 由a>b,得-2a<-2b | D. | 由a>b,得a2>b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
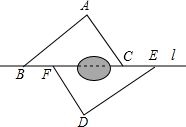 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y-$\frac{1}{y}$-3=0 | B. | y-$\frac{4}{y}$-3=0 | C. | y-$\frac{1}{y}$+3=0 | D. | y-$\frac{4}{y}$+3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com