
分析 首先计算括号内的分式,把第二个分式的分子和分母分解因式,然后把除法转化为乘法计算即可.
解答 解:(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$
=$\frac{x-2}{x-1}$÷$\frac{(x-2)^{2}}{(x+1)(x-1)}$
=$\frac{x-2}{x-1}$•$\frac{(x+1)(x-1)}{(x-2)^{2}}$
=$\frac{x+1}{x-2}$.
点评 本题考查了分式的混合运算,分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | B3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a是实数,|a|≥0 | |
| B. | 掷一枚硬币,正面朝上 | |
| C. | 某运动员跳高的最好成绩是20.1m | |
| D. | 从车间刚生产的产品中任意抽取一个,是次品 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
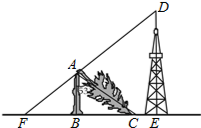 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成60°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成60°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com