
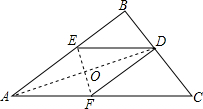
 如图,在三角形纸片ABC中,∠BAC为锐角,AB=12cm,AC=15cm.按下列步骤折叠:第一次,把∠B折叠使点B落在AC边上,折痕为AD,交BC于点D;第二次折叠,使点A与点D重合,折痕分别交AB、AC于点E、F,EF与AD交于点O,展开后,连结DE、DF.
如图,在三角形纸片ABC中,∠BAC为锐角,AB=12cm,AC=15cm.按下列步骤折叠:第一次,把∠B折叠使点B落在AC边上,折痕为AD,交BC于点D;第二次折叠,使点A与点D重合,折痕分别交AB、AC于点E、F,EF与AD交于点O,展开后,连结DE、DF.分析 (1)如图,首先证明∠OFA=∠OEA,得到AE=AF,此为解题的关键性结论;运用翻折变换的性质得到
AE=DE,AF=DF,即可解决问题.
(2)如图,首先证明△BED∽△BAC,得到$\frac{BE}{BA}=\frac{DE}{AC}$,进而证明$\frac{12-AF}{12}=\frac{AF}{15}$,求出AF,即可解决问题.
解答  解:(1)四边形AEDF是菱形.
解:(1)四边形AEDF是菱形.
理由:由第一次以AD为折痕的折叠可知:
∠OAF=∠OAE;
由第二次以EF为折痕的折叠可知:
AE=DE,AF=DF,∠AOE=90°,
∴∠OAF+∠OFA=90°,∠OAE+∠OEA=90°,
∴∠OFA=∠OEA,
∴AE=AF,
∴AE=DE=AF=DF,
∴四边形AEDF是菱形.
(2)由(1)知四边形AEDF是菱形,
∴DE∥AC,AE=AF=DE,
∴△BED∽△BAC,
∴$\frac{BE}{BA}=\frac{DE}{AC}$
∵AB=12cm,AC=15cm,
∴$\frac{12-AF}{12}=\frac{AF}{15}$,
∴AF=$\frac{20}{3}$(cm).
点评 该题主要考查了翻折变换的性质、菱形的判定、相似三角形的判定及其应用等几何知识点及其应用问题;深入观察图形,准确把握图形中隐含的数量关系是基础;灵活运用翻折变换的性质、相似三角形的判定及其应用等是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
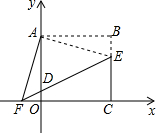 如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.
如图,在平面直角坐标系中,正方形OABC的点A在y轴上,点C在x轴上,点B(4,4),点E在BC边上,将△ABE绕点A顺时针旋转90°,得△AOF,连接EF交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
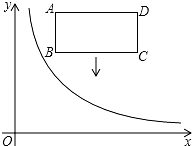 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )
如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数是( )| A. | 53° | B. | 55° | C. | 57° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1<x2<x3<x4 | B. | x1<x3<x4<x2 | C. | x3<x4<x1<x2 | D. | x3<x1<x2<x4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com