练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    25、阅读下列解题过程：
    如图，已知AB∥CD，∠B=35°，∠D=32°，求∠BED的度数．
    解：过E作EF∥AB，则AB∥CD∥EF（平行的传递性）
    AB∥EF?∠B=∠1=35°
    又因为CD∥EF?∠D=∠2=32°
    所以∠BED=∠BED=∠1+∠235°+32°=67°（等量代换）
    然后解答下列问题：
    如图，是明明设计的智力拼图玩具的一部分，现在明明遇到两个问题，请你帮他解决：
    问题（1）：∠D=30°，∠ACD=65°，为了保证AB∥DE，∠A=
    35°
    ；
    问题（2）：∠G+∠F+∠H=
    360
    °时，GP∥HQ．
    分析：本题主要利用两直线平行，同旁内角互补以及两直线平行内错角相等进行做题．
    解答：解：（1）由例题的结论可知，若AB∥DE，则∠A=∠ACD-∠D=65°-30°=35°；

    （2）过F作FE∥GP，若GP∥HQ，则FE∥GP∥HQ，
    ∠1+∠G=180°，∠2+∠H=180°，
    ∴∠1+∠2+∠G+∠H=360°，
    即∠G+∠F+∠H=360°．
    点评：两直线平行时，应该想到它们的性质，由两直线平行的关系得到角之间的数量关系，从而达到解决问题的目的．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    精英家教网（体验探究题）阅读下列解题过程并填空．
    如图所示，是一个转盘，转盘分成了6个相同的扇形，扇色有红、黄、蓝三种颜色，指针的位置固定，转动转盘后让其自动停止，其中的某个扇形会恰好停在指针所在的位置，求下列事件的概率．
    （1）事件A，指针指向红色．
    （2）事件B，指针指向红色或蓝色．
    解：设每个扇形面积为1个单位，问题中可能出现的均等结果有6种情况，所以n=6（单位）．
    （1）指针指向红色，出现红色所占面积m1，则m1=
     
    ，P（A）=
    m1
    n
    =
     
    ．
    （2）指针指向蓝色或红色，红色，蓝色所占面积m2=
     
    ，P（B）=
    m2
    n
    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （2013•安庆一模）阅读下列解题过程，并解答后面的问题：
    如图1，在平面直角坐标系xOy中，A（x1，y1），B（x2，y2），C为线段AB的中点，求C点的坐标．
    解：分布过A、C做x轴的平行线，过B、C做y轴的平行线，两组平行线的交点如图1所示．
    设C（x0，y0），则D（x0，y1），E（x2，y1），F（x2，y0）
    由图1可知：x0=
    x2-x1
    2
    +x1    =
    x1+x2
    2

    y0=
    y2-y1
    2
    +x1    =
    y1+y2
    2

    ∴（
    x1+x2
    2
    ，
    y1+y2
    2
    ）
    问题：（1）已知A（-1，4），B（3，-2），则线段AB的中点坐标为
    （1，1）
    （1，1）
    ．
    （2）平行四边形ABCD中，点A、B、C的坐标分别为（1，-4），（0，2），（5，6），求点D的坐标．
    （3）如图2，B（6，4）在函数y=
    1
    2
    x+1的图象上，A（5，2），C在x轴上，D在函数y=
    1
    2
    x+1的图象上，以A、B、C、D四个点为顶点构成平行四边形，直接写出所有满足条件的D点的坐标．

    查看答案和解析>>

    科目：初中数学 来源：活学巧练　　七年级数学　下 题型：044

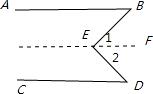
    阅读下列解题过程．

    如图(a)，已知，AB∥CD，∠B＝，∠D＝，求∠BED的度数．

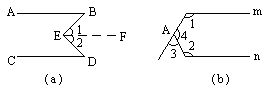
    　　解：过点E作EF∥AB(过直线外一点有且只有一条直线与已知直线平行)，

    　　∴∠1＝∠B(两直线平行，内错角相等)．

    　　∵AB∥CD，∴EF∥CD(平行于同一直线的两直线平行)．

    　　∴∠2＝∠D(两直线平行，内错角相等)．

    　　∴∠BED＝∠1＋∠2＝∠D＋∠B＝＋＝．

    请仿照上述解法，解答下列问题：

    如图(b)，m∥n，∠1＝，∠2＝，求∠3的度数．

    同伴间互相交流解题体会，看能否发现其中包含了哪些规律．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    阅读下列解题过程：
    如图，已知AB∥CD，∠B=35°，∠D=32°，求∠BED的度数．
    解：过E作EF∥AB，则AB∥CD∥EF（平行的传递性）
    AB∥EF?∠B=∠1=35°
    又因为CD∥EF?∠D=∠2=32°
    所以∠BED=∠BED=∠1+∠235°+32°=67°（等量代换）
    然后解答下列问题：
    如图，是明明设计的智力拼图玩具的一部分，现在明明遇到两个问题，请你帮他解决：
    问题（1）：∠D=30°，∠ACD=65°，为了保证AB∥DE，∠A=______；
    问题（2）：∠G+∠F+∠H=______°时，GP∥HQ．

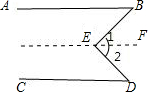
    查看答案和解析>>

    同步练习册答案